目录

1.按之字形顺序打印二叉树

 2.二叉树的最大深度

3. 二叉树中和为某一值的路径(一)

4.二叉搜索树与双向链表

 5.  对称的二叉树

1.按之字形顺序打印二叉树

其实就是二叉树层序遍历，只不过奇数层需要反转（用reverse）

层序遍历昨天讲过的层序以及前中后序

class Solution {
public:void level(vector>& vv, TreeNode* root, int depth)  {if (!root) return;if (vv.size() > depth)vv[depth].push_back(root->val);else{vector v;v.push_back(root->val);vv.push_back(v);}level(vv, root->left, depth + 1);level(vv, root->right, depth + 1);}vector > Print(TreeNode* pRoot) {vector> vv; //创建二维数组level(vv, pRoot, 0);  //层序for (int i = 0; i < vv.size(); i++){if (i % 2) //奇数层逆置reverse(vv[i].begin(), vv[i].end());}return vv;}
};

 2.二叉树的最大深度

二叉树的最大深度=左子树的最大深度+右子树的最大深度+1（根）

当然空树直接返回0

   int maxDepth(TreeNode* root) {// write code hereif(!root) return 0;int a1=maxDepth(root->left);int a2=maxDepth(root->right);return max(a1,a2)+1;}

3. 二叉树中和为某一值的路径(一)

只要一条路径符合就可以每次走过一条路径上的第一个非空节点，我们就从sum中减去节点值

最后当节点为空，返回false（说明走到空之后sum还没有被减空），如果左右都为空（走到当前路径最后一个节点上），判断sum和val是否相等

    bool hasPathSum(TreeNode* root, int sum) {// write code hereif(!root ) return false;if(!root->left && !root->right) return root->val==sum;return  hasPathSum(root->left, sum-root->val)||hasPathSum(root->right, sum-root->val);}

4.二叉搜索树与双向链表

这个题可以看成中序遍历的变式

找左，一直往左走，根的时候加上双向链表的链接，并且链接一个删除一个栈内节点，然后走左

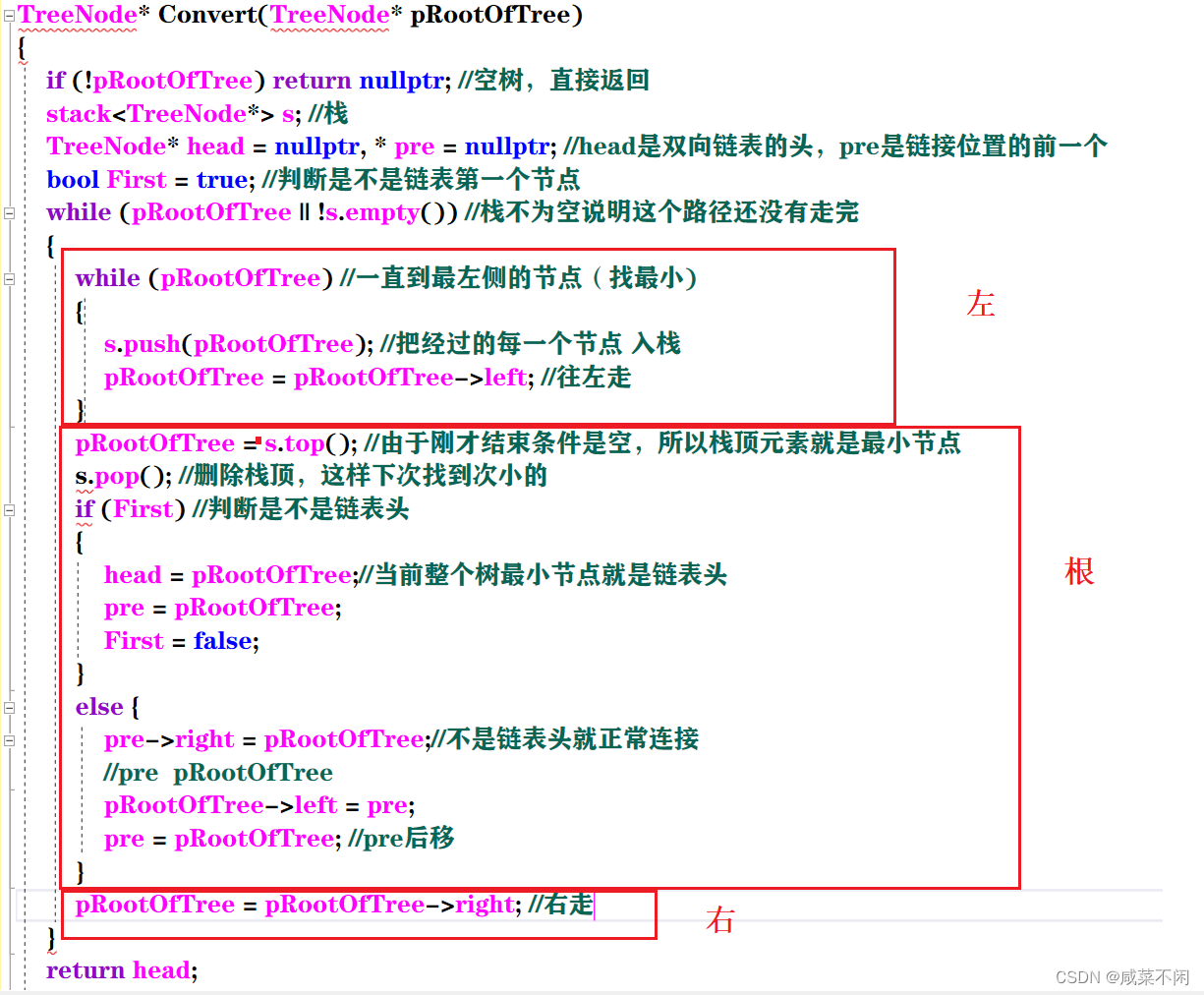
TreeNode* Convert(TreeNode* pRootOfTree)
{if (!pRootOfTree) return nullptr; //空树，直接返回stack s; //栈TreeNode* head = nullptr, * pre = nullptr; //head是双向链表的头，pre是链接位置的前一个bool First = true; //判断是不是链表第一个节点while (pRootOfTree || !s.empty()) //栈不为空说明这个路径还没有走完{while (pRootOfTree) //一直到最左侧的节点（找最小){s.push(pRootOfTree); //把经过的每一个节点 入栈pRootOfTree = pRootOfTree->left; //往左走}pRootOfTree = s.top(); //由于刚才结束条件是空，所以栈顶元素就是最小节点s.pop(); //删除栈顶，这样下次找到次小的if (First) //判断是不是链表头{head = pRootOfTree;//当前整个树最小节点就是链表头pre = pRootOfTree;First = false;}else {pre->right = pRootOfTree;//不是链表头就正常连接//pre  pRootOfTree pRootOfTree->left = pre;pre = pRootOfTree; //pre后移}pRootOfTree = pRootOfTree->right; //右走}return head;
}

当然中序可以写成递归

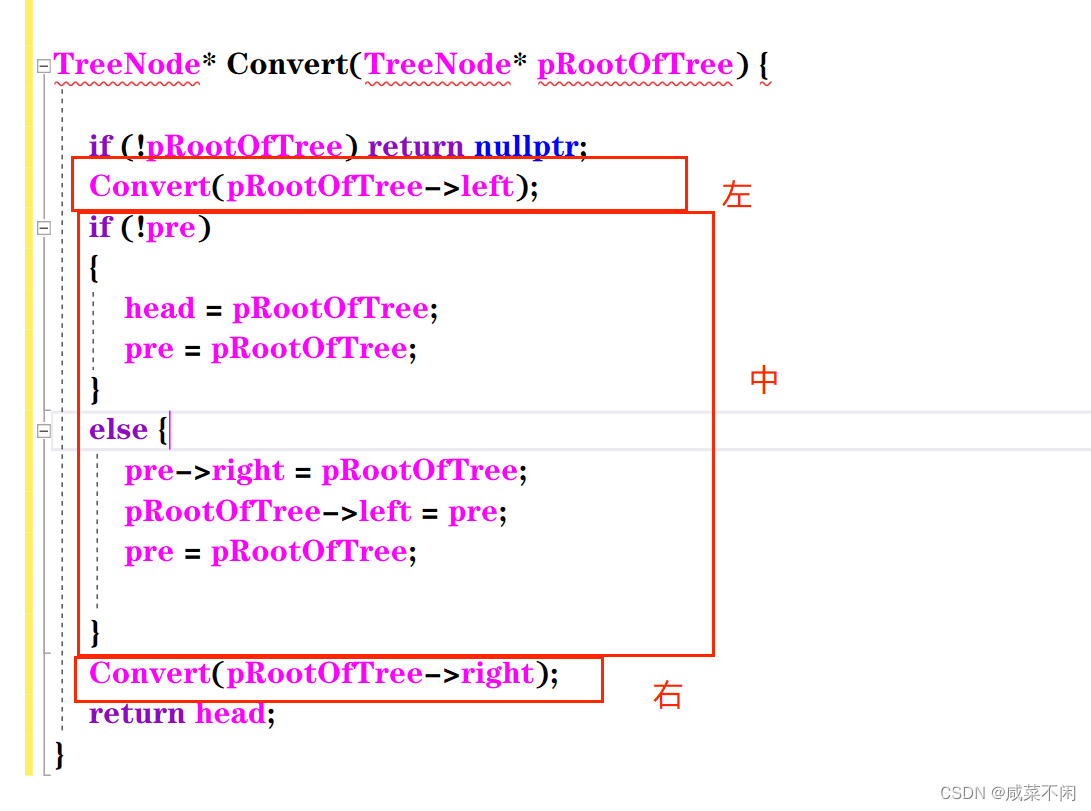
TreeNode* Convert(TreeNode* pRootOfTree) {if (!pRootOfTree) return nullptr;Convert(pRootOfTree->left); if (!pre){head = pRootOfTree;pre = pRootOfTree;}else {pre->right = pRootOfTree;pRootOfTree->left = pre;pre = pRootOfTree;}Convert(pRootOfTree->right);return head;
}

 5.  对称的二叉树

分别比较左子树和右子树的每个节点

bool _isSymmetrical(TreeNode* p1, TreeNode* p2) {if (!p1 && !p2) return true; //两个节点都是空，trueif ((p1 && !p2) || (!p1 && p2) || (p1->val != p2->val)) return false;//一个空另一个不空或者两个节点值不一样都falsereturn _isSymmetrical(p1->left, p2->right) && //看镜像而不是看对称_isSymmetrical(p1->right, p2->left);}
bool isSymmetrical(TreeNode* pRoot) {if (!pRoot) return true; //空树自然镜像return _isSymmetrical(pRoot->left, pRoot->right);
}