考研数二第五讲 无穷小阶数问题的求解
迪丽瓦拉
2025-05-30 06:54:09
0次
无穷小阶数问题的求解
在考研复习中，关于无穷小阶数的问题是比较多的，从最基本的确定无穷小阶数问题，到无穷小之间的阶数 比较问题，都是属于比较常见的类型。此外，还有一些其他的切入点的题目，值得多多注意。
题目没有说明具体是多少阶，而是让我们自己去尽可能确定无穷小的阶数，这种问法就相对来说比较有新意。最好的解法还是麦克劳林展开式：
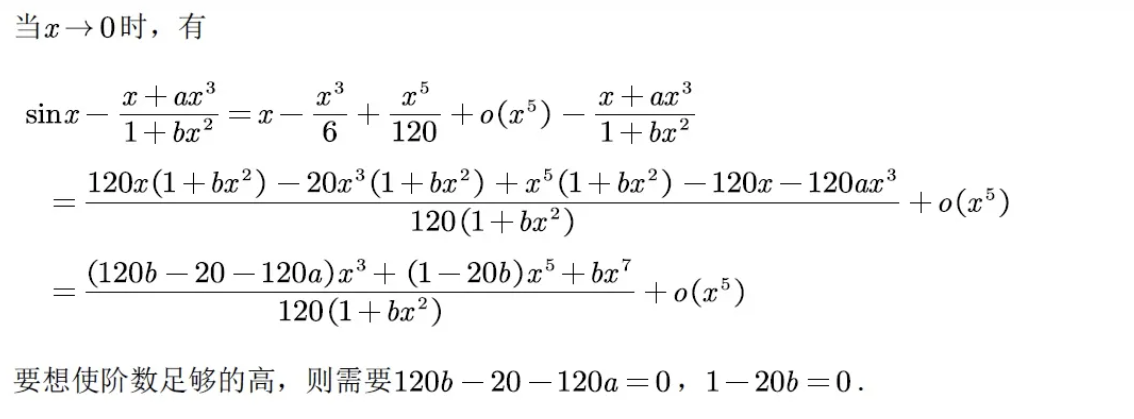
要想使阶数足够的高，就要尽可能使低阶项的系数为0，通过解方程求得结果。
关于无穷小阶数的问题，常规的做法一般都是借助麦克劳林展开式进行展开，确定第一个系数不为零的最低阶数，最终确定无穷小的阶数。除此以外，还有一种做法不常见，但也很值得学习，下题就是一个非常典型的例子。
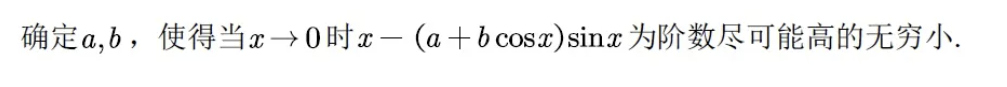
所以另y'(0)=y'''(0)=0
利用了一般函数的麦克劳林展开式，并令低阶导数尽可能等于0，确定未知参数，这样就达到题干中的无穷小阶数尽可能小的要求，也是值得借鉴的做法
一个常见函数的等价无穷小
有一个常见函数，它在考研里出现的几率极高，由它带出来的性质也比较多，今天会看到它的一个关于等价无穷小的性质，后续我们还会看到它在其他章节知识的出场。请看下题：
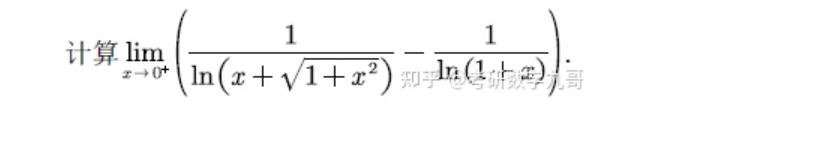
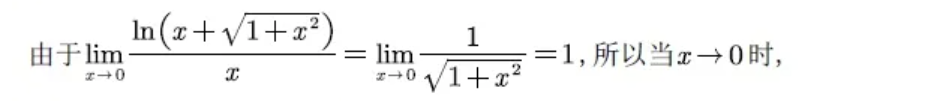
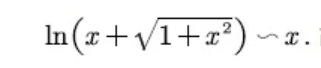
所以原题可得：
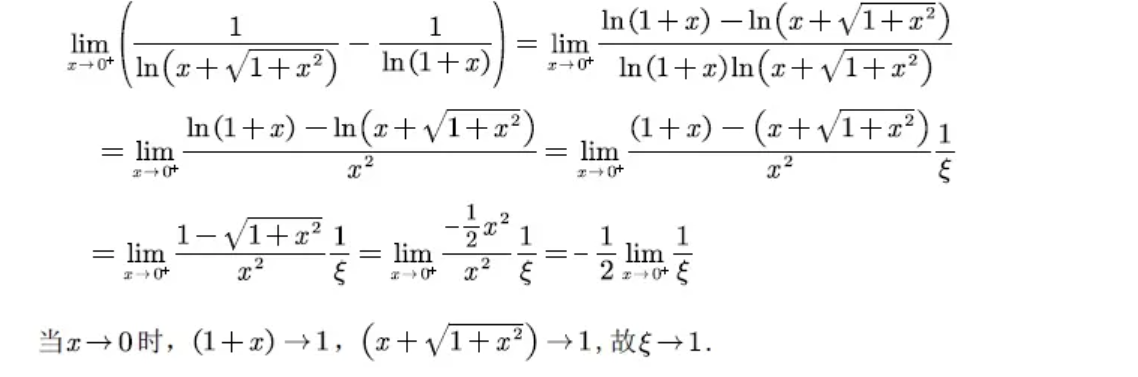
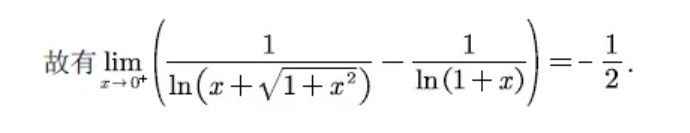
所说的这个等价无穷小，就是如下的这个：
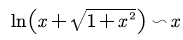
上一篇：助力近400家中国企业上云出海，博思云为有着怎样的心得体会？
下一篇：【C++】面试101，按之字形顺序打印二叉树,二叉树的最大深度, 二叉树中和为某一值的路径(一),二叉搜索树与双向链表, 对称的二叉树
相关内容
热门资讯
linux入门---制作进度条
了解缓冲区 我们首先来看看下面的操作： 我们首先创建了一个文件并在这个文件里面添加了...
C++ 机房预约系统（六）：学...
8、 学生模块 8.1 学生子菜单、登录和注销 实现步骤： 在Student.cpp的...
A.机器学习入门算法（三）：基...
机器学习算法（三）：K近邻(k-nearest neigh...
数字温湿度传感器DHT11模块...
模块实例https://blog.csdn.net/qq_38393591/article/deta...
有限元三角形单元的等效节点力
文章目录前言一、重新复习一下有限元三角形单元的理论1、三角形单元的形函数（Nÿ...
Redis 所有支持的数据结构...
Redis 是一种开源的基于键值对存储的 NoSQL 数据库，支持多种数据结构。以下是...
win下pytorch安装—c...
安装目录一、cuda安装1.1、cuda版本选择1.2、下载安装二、cudnn安装三、pytorch...
MySQL基础-多表查询
文章目录MySQL基础-多表查询一、案例及引入1、基础概念2、笛卡尔积的理解二、多表查询的分类1、等...
keil调试专题篇
调试的前提是需要连接调试器比如STLINK。 然后点击菜单或者快捷图标均可进入调试模式。 如果前面...
MATLAB | 全网最详细网...
一篇超超超长，超超超全面网络图绘制教程，本篇基本能讲清楚所有绘制要点&#...