例：f(n)=0.001n²-10n-1000=Ω(n²)
因为lim^n->∞f(n)/n²=0.001>0

f(n)=O(g(n))且f(n)=Ω(g(n)) =>f(n)=Θ(g(n))
证明法一：lim^n->∞^|f(n)/g(n)|=c，00，可求得n0值，从而存在c0和n0使得n^2是10n^2+3n+100的渐进上界；
同理，c1=9，10n^2+3n+100>9n^2即n^2+3n+100>0，可求得n1值，
从而存在c1和n1使得n^2是10n^2+3n+100的渐进下界；

渐进分析的常用等式：

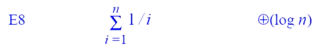
推导规则：


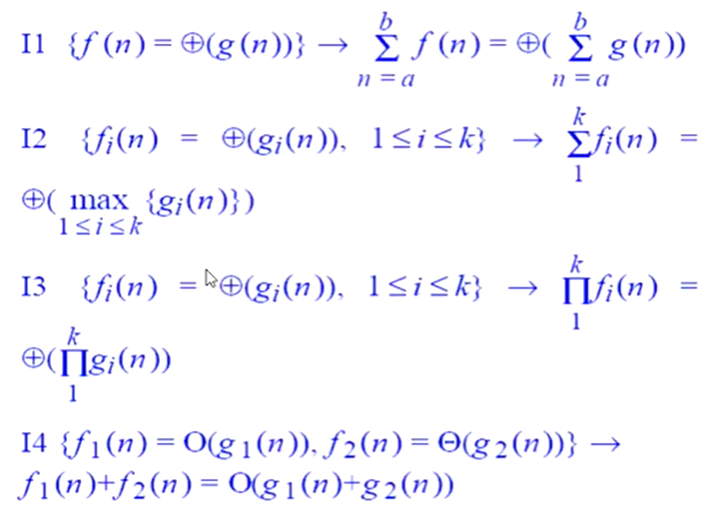
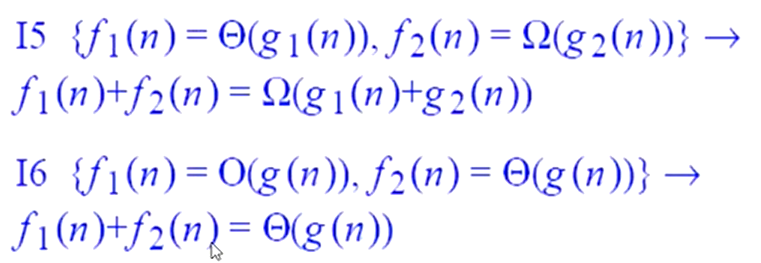
渐进分析例题：


Sum(a,n)共有2n+3步，b[j]=Sum(a,j+1)有2(j+1)+3+1=2j+6步，∑(j=0,n-1)2j+6=n²+5n=Θ(n²)
顺序查找：

插入排序、选择排序和rank排序最坏情形时间复杂度是O(n^2)，准确来说是Θ(n ^2)，平均情形时间复杂度是Θ(n ^2)
多项式时间算法：
如果一算法的最坏情形时间复杂度t(n)=O(n^k)，则称该算法为多项式时间复杂度的算法或有多项式界的算法；
如果一算法的最坏情形时间复杂度t(n)不能用多项式限界，则称该算法为指数复杂度的算法，认为是不可行的算法，这类问题称为NP-难度问题。

**解递归的三种方法：**

（1）递归树 （2）迭代 （3）主项法
归并排序：
归并已排好序的数组（MERGE）：

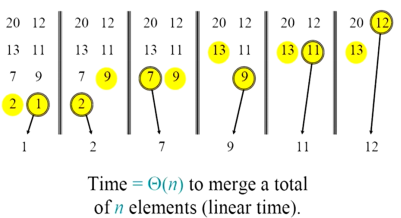
伪代码：

MERGE-SORT A[1，……，n]                     T(n)
1.if n=1 done.                             Θ(1)
2.Recursively sort A[1，……，[n/2]]         2T(n/2)and A[ [n/2]+1，……，n]
3.Merge the two sorted lists               Θ(n)

递归方程：

T(n)=Θ(1)  if  n=1=T(n/2)+Θ(n) if n>1

隐含假设n=2^h
用cn代替Θ(n)，不影响渐进分析的结果
递归树：

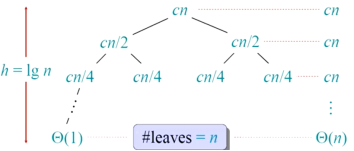
复杂度：cnlgn+Θ(n)=>Θ(nlgn)

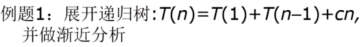
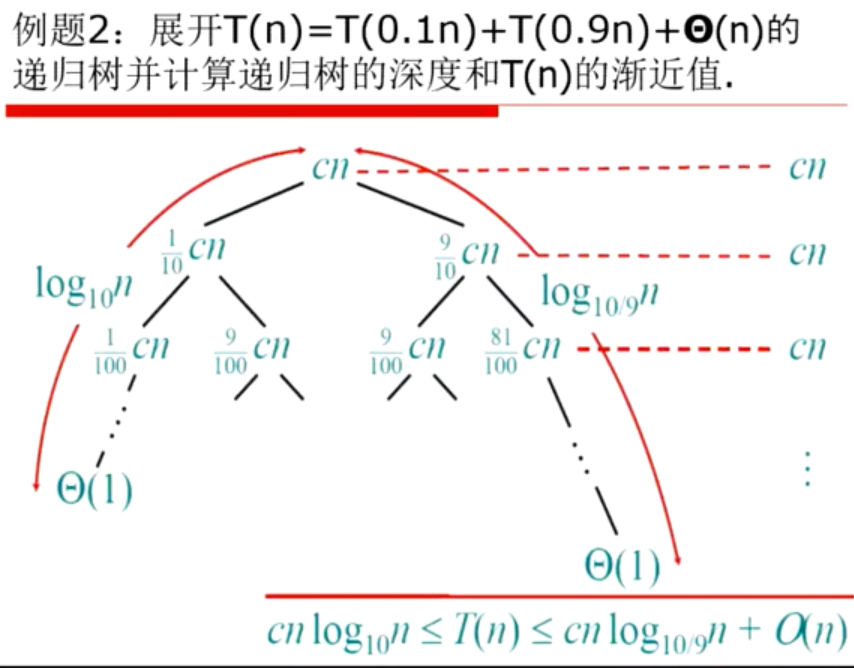
迭代展开：

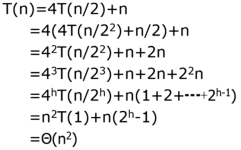
归并排序渐进优于插入排序。
递归树等价于迭代展开
很多递归式用递归树解不出来，但递归树能提供直觉，帮助我们用归纳法求解
主项法：
T(n)=aT(n/b)+f(n)
声明：logb,a表示以b为底a的对数
情形一：
f(n)=O(n^logb,a-ε)，ε>0为某一常数
则T(n)=Θ(n^logb,a)
情形二：
f(n)=Θ(n^logb,alg^kn), k>=0为某一常数
则T(n)=Θ(n^logb,alg^k+1n)
情形三：
f(n)=Ω(n^logb,a+ε)，ε>0为某一常数
则T(n)=Θ(f(n))