文章目录

• k 近邻算法（分类）
• k 近邻模型
• • 模型
  • 距离度量
  • k 值的选择
  • 分类决策规则
• k 近邻法的实现：kd 树
• • 构造 kd 树
  • 搜索 kd 树
• References

k 近邻法（k-nearest neighbor, KNN）是一种基本分类与回归方法。分类时，k 近邻法的输入为实例的特征向量，对应于特征空间的点；输出为实例的类别，可以取多类。其背后的原理是从训练样本中找到与新点在距离上最近的预定数量（k）的几个点，通过多数表决等方式进行预测，距离可以通过任何度量来衡量，最常见的选择是标准欧式距离（standard Euclidean distance）。因此，k 值的选择、距离度量及分类决策规则是 KNN 的三个基本要素，KNN 不具有显式的学习过程。

k 近邻算法（分类）

输入：训练数据集
T=(x1,y1),(x2,y2),⋯,(xN,yN)T={(x_1,y_1), (x_2,y_2), \cdots,(x_N,y_N)} T=(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)
其中，xi∈Xx_i \in \mathcal{X}xi​∈X 为实例的特征向量，yi∈Y={c1,c2,⋯,cK}y_i \in \mathcal{Y}=\{c1,c2,\cdots,c_K\}yi​∈Y={c1,c2,⋯,cK​} 为实例的类别。

输出：实例 xxx 所属的类 yyy。

1. 根据给定的距离度量，在训练集 TTT 中找出与 xxx 最邻近的 kkk 个点，涵盖这 kkk 个点的 xxx 的邻域记作 Nk(x)N_k(x)Nk​(x)；
2. 在 Nk(x)N_k(x)Nk​(x) 中根据分类决策规则（如多数表决）决定 xxx 的类别 yyy：
   y=arg max⁡cj∑xi∈Nk(x)I(yi=cj),i=1,2,⋯,k,j=1,2,⋯,Ky=\argmax_{c_j}\sum_{x_i\in N_k(x)}I(y_i=c_j),\quad i=1,2,\cdots,k,\ j=1,2,\cdots,K y=cj​argmax​xi​∈Nk​(x)∑​I(yi​=cj​),i=1,2,⋯,k, j=1,2,⋯,K
   其中 III 为指示函数，即当 yi=cjy_i=c_jyi​=cj​ 时 III 为 1，否则为 0.

k 近邻法的特殊情况是 k=1k=1k=1 的情形，称为最近邻算法。最近邻算法将训练数据集中与 xxx 最邻近点的类作为 xxx 的类。如果邻居 k+1k+1k+1 和邻居 kkk 具有相同的距离，但具有不同的标签，结果将取决于训练数据的顺序。

为了完成找到两组数据集中最近邻点的简单任务，可以使用 sklearn.neighbors 中的无监督算法，NearestNeighbors 实现了无监督的最近邻学习，它为三种不同的最近邻算法（kd树（稍后介绍），ball 树以及暴力算法）提供统一的接口，算法的选择可以通过关键字 algorithm 来控制，当设置为默认值 auto 时，算法会尝试从训练数据中确定最佳方法：

from sklearn.neighbors import NearestNeighbors
import numpy as npX = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([[1, -1], [3, 2], [2, 2]])
nbrs = NearestNeighbors(n_neighbors=1, algorithm='ball_tree').fit(X)
distances, indices = nbrs.kneighbors(Y)indices
"""
array([[0],[5],[4]])
"""distances
"""
array([[2.],[0.],[1.]])
"""

结果表明，X 数据集中离 Y 数据集中点 [1, -1] 最近的点为 [-1, -1]，距离为 2；离 Y 数据集中点 [3, 2] 最近的点为 [3, 2]，距离为 0；离 Y 数据集中点 [2, 2] 最近的点为 [2, 1]，距离为 1。

k 近邻模型

模型

k 近邻法中，当训练集、距离度量、kkk 值及分类决策规则确定后，对于任何一个新的输入实例，它所属的类唯一地确定。这相当于根据上述要素将特征空间划分为一些子空间，确定子空间里的每个点所属的类。

特征空间中，对每个训练实例点 xix_ixi​，距离该点比其他点更近的所有点组成一个区域，叫做单元（cell）。每个训练实例点拥有一个单元，所有训练实例点的单元构成对特征空间的一个划分。最近邻法将实例 xix_ixi​ 的类 yiy_iyi​ 作为其单元中所有点的类标记。

距离度量

特征空间中两个实例点的距离是两个实例点相似程度的反映。假设特征空间 X\mathcal{X}X 是 nnn 维实数向量空间 Rn\mathbb{R}^nRn，xi,xj∈Xx_i,x_j \in \mathcal{X}xi​,xj​∈X，xi=(xi(1),xi(2),⋯,xi(n))x_i=(x_i^{(1)},x_i^{(2)}, \cdots,x_i^{(n)})xi​=(xi(1)​,xi(2)​,⋯,xi(n)​)，xj=(xj(1),xj(2),⋯,xj(n))Tx_j=(x_j^{(1)},x_j^{(2)}, \cdots,x_j^{(n)})^Txj​=(xj(1)​,xj(2)​,⋯,xj(n)​)T，xi,xjx_i,x_jxi​,xj​ 的 LpL_pLp​ 距离定义为
Lp(xi,xj)=(∑l=1n∣xi(l)−xj(l)∣p)1pL_p(x_i,x_j)=\left(\sum_{l=1}^n |x_i^{(l)} - x_j^{(l)}|^p \right)^{\frac{1}{p}} Lp​(xi​,xj​)=(l=1∑n​∣xi(l)​−xj(l)​∣p)p1​

这里 p≥1p \ge 1p≥1。当 p=2p=2p=2 时，称为欧氏距离，即
L2(xi,xj)=(∑l=1n∣xi(l)−xj(l)∣2)12L_2(x_i,x_j)=\left(\sum_{l=1}^n |x_i^{(l)} - x_j^{(l)}|^2 \right)^{\frac{1}{2}} L2​(xi​,xj​)=(l=1∑n​∣xi(l)​−xj(l)​∣2)21​

当 p=1p=1p=1 时，称为曼哈顿距离（Manhattan distance），即
L1(xi,xj)=∑l=1n∣xi(l)−xj(l)∣L_1(x_i,x_j)=\sum_{l=1}^n|x_i^{(l)} - x_j^{(l)}| L1​(xi​,xj​)=l=1∑n​∣xi(l)​−xj(l)​∣

当 p=∞p=\inftyp=∞ 时，它是各个坐标距离的最大值，即
L∞(xi,xj)=max⁡l∣xi(l)−xj(l)∣L_\infty(x_i,x_j) = \max_l |x_i^{(l)} - x_j^{(l)}| L∞​(xi​,xj​)=lmax​∣xi(l)​−xj(l)​∣

下图给出了二维空间中 ppp 取不同值时，与原点的 LpL_pLp​ 距离为 1 的点的图形。

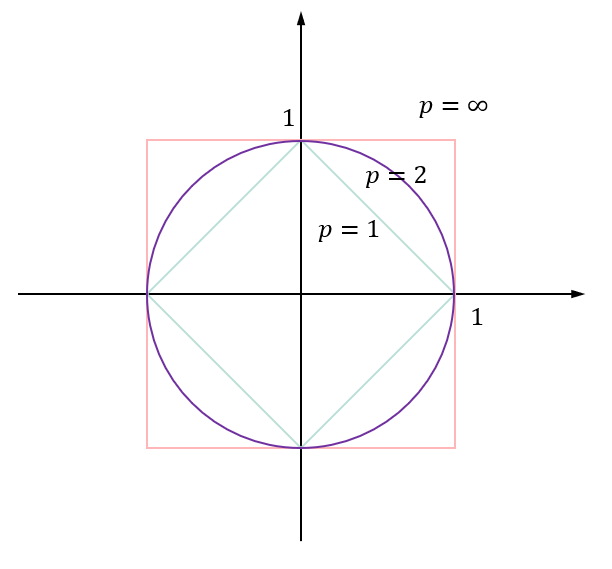
k 值的选择

如果选择较小的 k 值，就相当于用较小的邻域中的训练实例进行预测，学习的近似误差会减小，只有与输入实例较近的训练实例才会对预测结果起作用。但缺点是学习的估计误差会增大，预测结果会对近邻的实例点非常敏感，如果近邻的实例恰巧是噪声，预测就会出错。换句话说，k 值的减小意味着整体模型变得复杂，容易发生过拟合。

如果选择较大的 k 值，就相当于用较大的邻域中的训练实例进行预测。其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大，这时与输入实例较远的训练实例也会对预测起作用，使预测发生错误。k 值的增大意味着整体模型变得简单。

如果 k=Nk=Nk=N，那么无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类，这时模型过于简单，完全忽略训练实例中的大量有用信息，是不可取的。

在实际中，k 值一般取一个比较小的数值。通常采用交叉验证法来选取最优的 k 值。

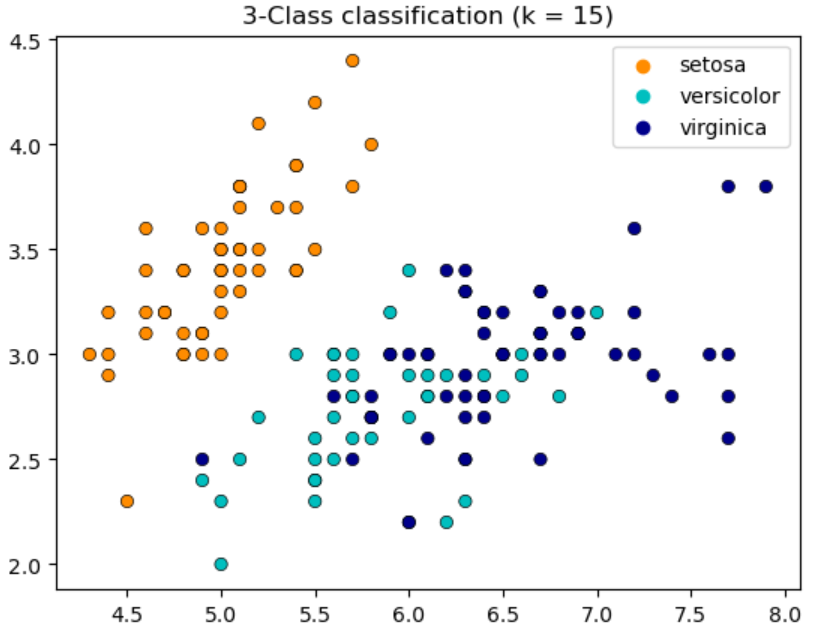
下面的代码使用不同的 k 值来对鸢尾花数据进行分类：

import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasetsiris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target# Create color maps
cmap_light = ListedColormap(["orange", "cyan", "cornflowerblue"])
cmap_bold = ["darkorange", "c", "darkblue"]for n_neighbors in [1, 5, 10, 15]:plt.figure()clf = neighbors.KNeighborsClassifier(n_neighbors)clf.fit(X, y)sns.scatterplot(x=X[:, 0],y=X[:, 1],hue=iris.target_names[y],palette=cmap_bold,alpha=1.0,edgecolor="black",)plt.title("3-Class classification (k = %i)" % (n_neighbors))

分类决策规则

k 近邻法中的分类决策规则往往是多数表决，即由输入实例的 k 个邻近的训练实例中的多数类决定输入实例的类。多数表决规则有如下解释：如果分类的损失函数为 0-1 损失函数，分类函数为
f:Rn→{c1,c2,⋯,cK}f:\mathbb{R}^n \to \{c1,c2,\cdots,c_K\} f:Rn→{c1,c2,⋯,cK​}

那么误分类的概率是
P(Y≠f(X))=1−P(Y=f(X))P(Y\neq f(X))=1-P(Y=f(X)) P(Y=f(X))=1−P(Y=f(X))

如果涵盖 Nk(x)N_k(x)Nk​(x) 的区域的类别是 cjc_jcj​，那么误分类概率是
1k∑xi∈Nk(x)I(yi≠cj)1−1k∑xi∈Nk(x)I(yi=cj)\frac{1}{k}\sum_{x_i\in N_k(x)}I(y_i\neq c_j)1-\frac{1}{k}\sum_{x_i\in N_k(x)}I(y_i=c_j) k1​xi​∈Nk​(x)∑​I(yi​=cj​)1−k1​xi​∈Nk​(x)∑​I(yi​=cj​)

要使误分类概率最小即经验风险最小，就要使 ∑xi∈Nk(x)I(yi=cj)\sum_{x_i\in N_k(x)}I(y_i=c_j)∑xi​∈Nk​(x)​I(yi​=cj​) 最大，所以多数表决规则等价于经验风险最小化。

k 近邻法的实现：kd 树

实现 k 近邻法时，主要考虑的问题是如何对训练数据进行快速 k 近邻搜索。最简单的实现方法是线性扫描，这时要计算输入实例与每一个训练实例的距离，当训练集很大时，计算非常耗时，这种方法是不可行的。

为了提高 k 近邻搜索的效率，可以考虑使用特殊的结构存储训练数据，以减少计算距离的次数。kd 树是方法之一。

构造 kd 树

kd 树是一种对 k 维空间中的实例点进行存储以便对齐进行快速检索的树形数据结构。kd 树是二叉树，表示对 k 维空间的一个划分。

构造平衡 kd 树算法：

输入：k 维空间数据集 T={x1,x2,⋯,xN}T=\{x_1,x_2,\cdots,x_N\}T={x1​,x2​,⋯,xN​}，其中 xi=(xi(1),xi(2),⋯,xi(k))Tx_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(k)})^\text{T}xi​=(xi(1)​,xi(2)​,⋯,xi(k)​)T.

输出：kd 树

1. 开始：构造根结点，根结点对应于包含 TTT 的 k 维空间的超矩形区域。
   
   选择 x(1)x^{(1)}x(1) 为坐标轴，以 TTT 中所有实例的 x(1)x^{(1)}x(1) 坐标的中位数为切分点，将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 x(1)x^{(1)}x(1) 垂直的超平面实现。
   
   由根结点生成深度为 1 的左、右子结点：左子结点对应坐标 x(1)x^{(1)}x(1) 小于切分点的子区域，右子结点对应坐标 x(1)x^{(1)}x(1) 大于切分点的子区域。
   
   将落在切分超平面上的实例点保存在根结点。
   

2. 重复：对深度为 j 的结点，选择 x(l)x^{(l)}x(l) 为切分的坐标轴，l=j(mod k)+1l=j\ (\text{mod}\ k) + 1l=j (mod k)+1，以该结点的区域中所有实例的 x(l)x^{(l)}x(l) 坐标的中位数为切分点，将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 x(l)x^{(l)}x(l) 垂直的超平面实现。
   
   由该结点生成深度为 j+1j+1j+1 的左、右子结点：左子结点对应坐标 x(l)x^{(l)}x(l) 小于切分点的子区域，右子结点对应坐标 x(l)x^{(l)}x(l) 大于切分点的子区域。
   
   将落在切分超平面上的实例点保存在该结点

3. 直到两个子区域没有实例存在时停止，从而形成 kd 树的区域划分。

例子：给定一个二维空间的数据集
T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}T=\{(2, 3), (5, 4), (9,6),(4, 7),(8,1),(7,2)\} T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}构造一个平衡 kd 树。

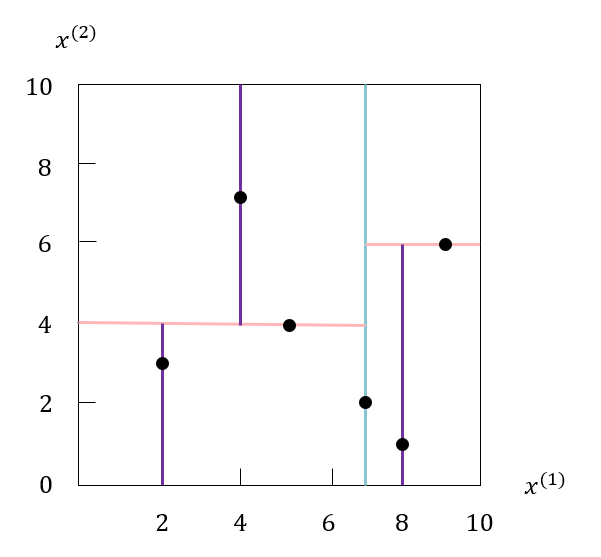
选择 x(1)x^{(1)}x(1) 轴，6 个数据点的 x(1)x^{(1)}x(1) 坐标的中位数是 7，以平面 x(1)=7x^{(1)}=7x(1)=7 将空间分为左、右两个子结点（子矩形）；接着，左矩形以 x(2)=4x^{(2)}=4x(2)=4 分为两个子矩形，右矩形以 x(2)=6x^{(2)}=6x(2)=6 分为两个子矩形，如此递归下去。

特征空间划分过程如下图所示：

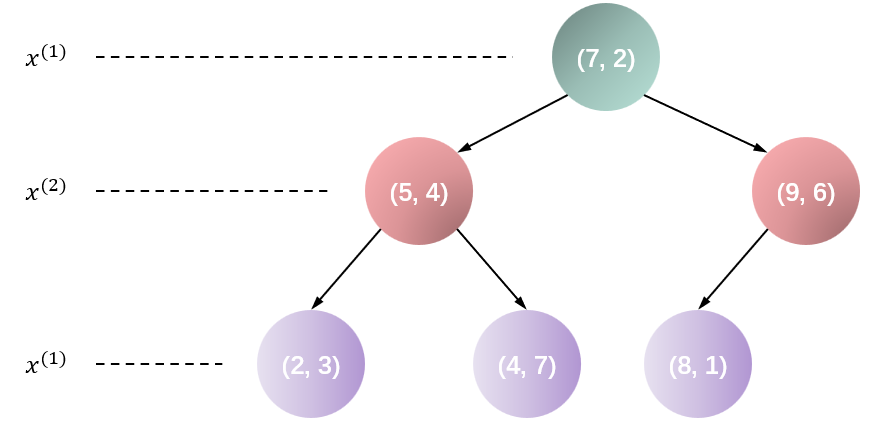
构造好的 kd 树如下图所示：

搜索 kd 树

利用 kd 树可以省去对大部分数据点的搜索，从而减少搜索的计算量。这里以最近邻为例，同样的方法可以应用到 k 近邻。

用 kd 树的最近邻搜索算法：

输入：已构造的 kd 树，目标点 xxx。

输出：xxx 的最近邻。

1. 在 kdkdkd 树中找出包含目标点 xxx 的叶结点：从根结点出发，递归地向下访问 kdkdkd 树。若目标点 xxx 当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点，直到子结点为叶结点为止。

2. 以此叶结点为“当前最近点”。

3. 递归地向上回退，在每个结点进行以下操作：
   
   (a) 如果该结点保存的实例点比当前最近点距离目标点更近，则以该实例点为“当前最近点”。
   
   (b) 当前最近点一定存在于该结点一个子结点对应的区域。检查该子结点的父结点的另一子结点对应的区域是否有更近的点。具体地，检查另一子结点对应的区域是否与以目标点为球心、以目标点与当前最近点间的距离为半径的超球体相交。如果相交，可能在另一个子结点对应的区域内存在距离目标点更近的点，移动到另一个子结点。接着，递归地进行最近邻搜索。如果不相交，向上回退。

4. 当回退到根结点时，搜索结束。最后的当前最近点即为 xxx 的最近邻点。

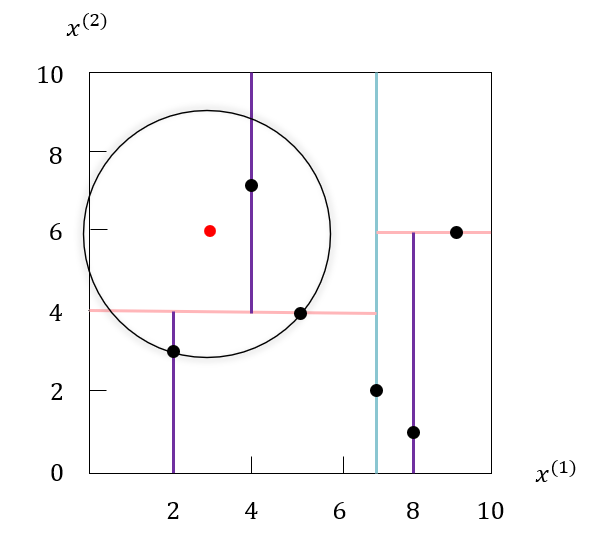
例如，我们根据上面构造出的 kdkdkd 树，寻找目标实例点 (3,6) 的最近邻。首先我们找到包含目标结点的叶结点 (2,3)，以点 (2,3) 作为当前最近点。

真正的最近邻一定再以点 (3,6) 为中心通过点 (2,3) 的圆的内部。然后返回结点 (2,3) 的父结点 (5,4)，在父结点 (5,4) 的另一子结点 (4,7) 的区域内搜索最近邻。结点 (4,7) 的区域与圆相交，且点 (4,7) 比 点 (2,3) 更近，(4,7) 成为新的当前最近点。

继续返回上一级父结点，即根结点 (7,2)，在根结点的另一子结点 (9,6) 的区域内搜索最近邻。结点 (9,6) 的区域与圆不相交，不可能有最近邻点。回退到根结点，搜索结束。当前最近点 (4,7) 即为目标点 (3,6) 的最近邻。

如果实例点是随机分布的，kdkdkd 树搜索的平均复杂度是 O(log⁡N)O(\log N)O(logN)，NNN 是训练实例数。 kdkdkd 树更适用于训练实例数远大于空间维数时的 k 近邻搜索。当空间维数接近训练实例数时，它的效率会迅速下降，几乎接近线性扫描，这就是所谓的维度灾难的一种体现。Ball 树的研究就是为了解决 kdkdkd 树 在高维上效率低下的问题。

References

[1] 《机器学习方法》，李航，清华大学出版社。
[2] sklearn 中文文档，https://www.sklearncn.cn/7/。