XOR, Tree, and Queries

大意：
给定一棵树n个节点，然后告诉你m个点对之间的简单路径异或和。要求构造出满足条件的一棵树，使得所有边权满足条件，且所有边权的异或和尽可能小

思路：

实在妙妙子，我看到构造所有边权就是直接傻眼，寻思线性基还是trie好像都不能给出构造方案。没想到题目只用了异或的最简单的性质，加上反常的建图，就解决了...

首先树上异或的话，一个常见的trick就是做根到节点的前缀异或和。我们记pi表示根节点到i的路径上的边权异或和，那么不难发现，对于任意两个节点u,v,它们之间的简单路径异或和可以按如下方式转化

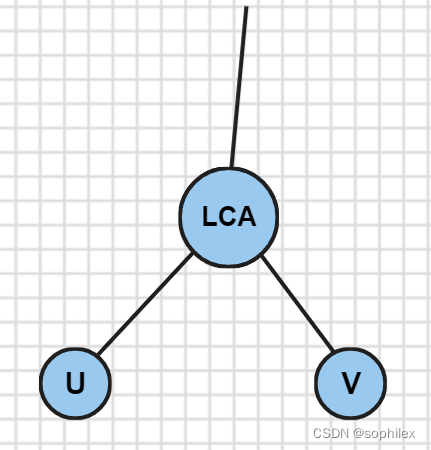
 等于u-lca的路径与lca-v的异或和，也就是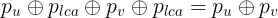

如果我们已知u到v的路径异或和是x，则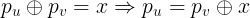

所以我们可以通过上述结论来尝试推出对应节点的值。

所以，我们可以按给的边权异或和关系来重新建图，这样会得到一个个连通块。每一个连通块内，我们从任意一个起点出发（不妨假设它的pi值为0，这当然是合理的，因为想要修改它为x的话，我们只要让连通块内的点的p值都异或上x就可以了。个人感觉这里并不好想，因为完全是在两个不同的图上面考虑，这里的修改权值意味着在树上一大段路径的修改。但是我们在推的时候肯定是保证了可行性，而我们不用找到具体的构造方案，只要它一定存在就可以了），可以推出其余点的p值，然后，如果里面有环，并且发现某一个点从不同路径走有不同值时，意味着该情况无解，这题就结束了。否则，我们就能得到一组满足条件的边权。

然后考虑题目的另一个约束条件：边权的异或和最小。

套用上述结论，对于相邻节点u，v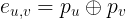，,所以我们可以将所求式子改写

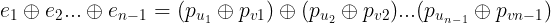
显然每一个pi有贡献当且仅当它出现次数为奇数，也就是i节点的度数为1

所以我们把所有度数为1的节点找出来，它们的异或和，就是我们的答案。

然后要优化的话，我们一定是在每一个连通块里统一异或上一个值。如果某一个连通块的大小是偶数，意味着我们要修改的值x会异或上偶数次，相当于没有操作。所以大小为偶数的连通块堆我们没帮助。

而一旦出现大小为奇数的连通块，也就是最后结果会异或上我们的修改值x。我们只要让x等于当前答案，那么最后的总体异或值就是0了。此时我们只要在该连通块内修改每一个点的p值，就能退出得到所有边权了。

所以，看起来是一道很伤脑筋的构造题，其实最后的结果只有三种情况：无解，0，一个常值。

至于前面的如何在一个连通块内推出所有值，dfs一下即可，有点像染色。我也看到过有人是拆开按位考虑，然后每一位就变成了0或者1的情况，那样就是二分图染色来标记了。

直接做的话，我们的复杂度可以来到喜人的O(n)

code

#include
using namespace std;
#define ll long long
#define endl '\n'
const ll N=3e5+10;
struct ty
{ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
void add(ll a,ll b,ll c)
{edge[++cn].t=b;edge[cn].l=c;edge[cn].next=head[a];head[a]=cn;
}
ll e1[N],e2[N];
ll fl[N];//度数为奇数的话就标记 
ll n,m;
ll vis[N];
ll p[N];//答案 
ll siz[N];
void dfs(ll id,ll k)
{vis[id]=k;for(int i=head[id];i!=-1;i=edge[i].next){ll y=edge[i].t;if(vis[y]==0){p[y]=p[id]^edge[i].l;dfs(y,k);}else if(p[y]!=(p[id]^edge[i].l)){cout<<"No"<>n>>m;for(int i=1;i>e1[i]>>e2[i];fl[e1[i]]^=1;fl[e2[i]]^=1;}for(int i=1;i<=m;++i){ll a,b,c;cin>>a>>b>>c;add(a,b,c);add(b,a,c);}for(int i=1;i<=n;++i){if(vis[i]) continue;dfs(i,i); }ll ans=0;for(int i=1;i<=n;++i){if(fl[i]) ans^=p[i],siz[vis[i]]++;}for(int i=1;i<=n;++i){if(siz[i]%2==0) continue;//cout<<"df "<