英文标题：Analysis of Parameterless Particle Swarm Algorithm for Traveling Salesman Problem

摘要

进化算法（EA）是标准的搜索机制，它使用自然选择和最佳生存作为基本的算法进展机制。无参数组合是一种特殊的技术，旨在解决各类问题，而不需要事先设置参数。这种技术涉及到计算工作量的增加，可以认为是可以接受的。在这项工作中，使用粒子群优化方法的无参数蜂群算法已被定义为旅行推销员问题的应用。通过应用无参数组合分析了该算法的性能，可以推断出，通过本工作中讨论的好处，可以证明使进化过程无参数化的努力是合理的。

简介：

进化算法是受自然界启发的算法，它在自然界中找到了灵感，并试图用数学术语设计一种行为[1]。这个数学公式背后的基本概念是进化。进化涉及四个重要的公设。

一个物种中的所有个体以某种形式是唯一的。

 在继续物种的过程中，变异被传递给下一代，称为后代。

 在一组个体中，产生的后代多于能存活的个体数量。

 世代的进展是基于自然选择的，它不是随机产生的。

进化计算技术利用进化算法的自然选择原理，应用于各种领域，如优化、机器学习、机器人、硬件设计和规划。这些技术与人工智能技术密切相关，因为它们参与了搜索过程。进化算法之所以受到欢迎，有几个原因，比如它们非常适合没有标准方法可供解决的问题。这些方法适用于多目标和多解优化方法。搜索机制对多个解决方案同时进行评估，从而产生更好的并行搜索。尽管EA有几个优点，但这种方法的主要缺点是固定算法参数的固有步骤，这通常是在试错的基础上进行的。所得到的解决方案是一个低于标准的解决方案，可以作为高效搜索过程或实现的初始选择。本文建议根据计算问题的条件，在各种算法中选择无参数进化算法。

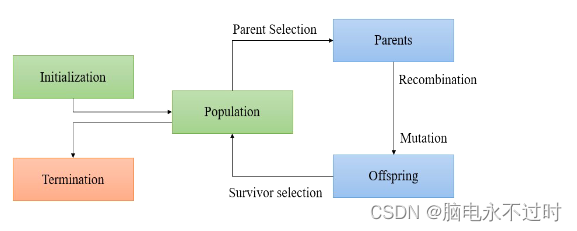
图一：进化算法的方框图。

图1所示的进化算法框图可以帮助我们理解自然选择的过程。进入进化过程的一组个体首先要经历初始化过程。这是为第一次迭代选择个体的方法。第一种群或零种群是随机选择的，因为个体的信息通常在初始阶段不存在。种群是指经过搜索过程以寻找最佳个体的一组个体。下一代是通过选择父母和重组从零人口发展起来的。个体的适合度是通过领域特定的适合度函数来测试的。重组确保了遗传信息的混合，从而使种群中充满了比上一代更好的个体。突变是一种在遗传信息中进行微小推动的算子，可以推动个体成为下一代的一部分。

进化算法可分为四大类：进化规划、进化策略、遗传算法和遗传规划。进化规划[2]包括通过随机变异选择允许的字母来修改的状态机形式。进化策略使用实值向量，并通过种群、突变和适应度评估创建更好的种群。

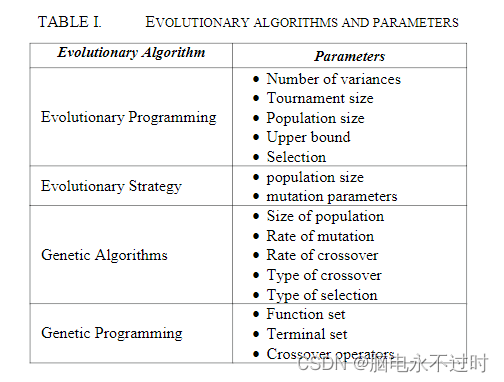
进化策略以收敛速度和可靠性而闻名[2]。遗传算法是自1975年以来最流行的EA。由于鲁棒性、收敛性和易于适应任何问题领域，它已经很好地适应了几个优化问题。选择、交叉和突变等遗传计算方法使遗传算法能够正常工作。遗传编程是EA的高级版本，使用符号、树和交叉来开发良好的表示。

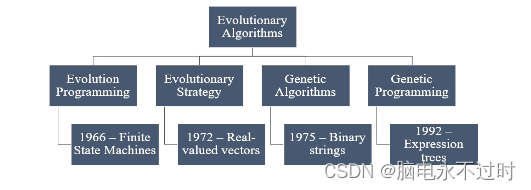
图2：进化算法的分类。

图2所示的EA分类法表明，从抽象表示（如有限状态机）到复杂的表达式树，搜索技术已经发展了一段时间。

群体算法（swam）是基于一组表现出繁殖、食物搜索或保护等特定行为的生物物种设计的。这种数学建模方法最初是在1989年以随机扩散搜索[3]的名义设计的，现在已经设计了更多这样的方法。群体算法中最流行的算法是粒子群优化（PSO）[4]。粒子群优化（PSO）是一种综合优化算法，专门处理最佳解通常表示为n维解空间中的一个空间点的问题。粒子群优化是通过问题维度、粒子数、加速度系数、惯性权重和迭代次数等参数唯一定义的。

根据问题的选定维度定义了解决方案空间。粒子在解决方案空间中导航，如图4所示。根据适合度标准对粒子进行评估。粒子被加速到具有更好适应度值的当前最佳粒子。粒子群优化算法利用一组粒子，形成在搜索空间中导航的粒子群。这个过程主要是为了寻找最佳解决方案。N维空间中的粒子根据其个人经验移动，并根据社会经验进行调整。个人最佳成绩被称为pbest。迄今为止最好的价值被称为全球最佳，gbest。PSO的基本概念包括加速每个粒子到达其pbest和gbest位置，每个时间步长都有一个非系统的加权加速度，如图3所示。

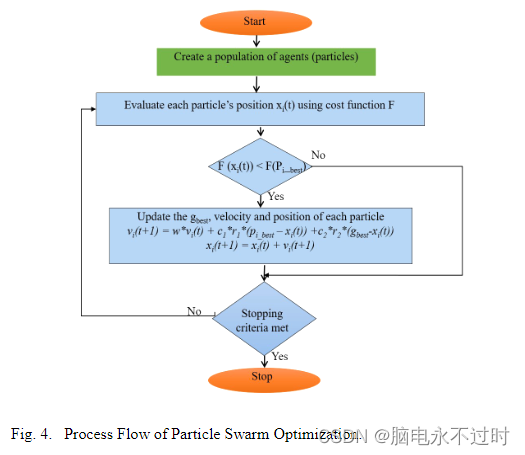
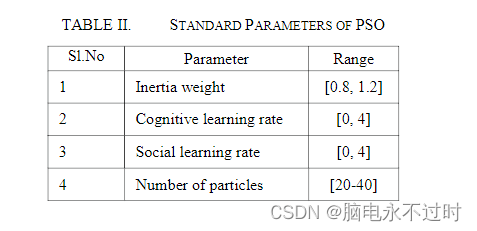
粒子群优化具有表2中列出的标准参数值。这些参数是通过大量问题的经验和试验来定义的。很容易从应用程序中避开这些参数。PSO不需要任何选择或交叉操作，并且没有为该特定算法定义适者生存。标准粒子群优化算法在整个过程中保持粒子的数量。

进化算法通常涉及一个或多个参数。当适当地选择这些参数时，这些参数使得算法能够有效地进行。选择的参数类似于深度学习中的超参数，在许多应用领域都是一项艰巨的任务。对参数选择和优化的需求推动了对无参数进化方法的研究。

PSO已成功实施的一些应用程序如下所示：

神经网络训练

–帕金森病的检测[6]。

–从模糊网络中提取规则[7]

–图像识别[8]

 电力优化分配[9]

 结构优化

–最佳形状和尺寸设计[10]

–图形结构优化[11]

 生物力学系统识别

如果参数可以动态选择，并且这个概念是这项工作的核心，那么可以减少参数的问题。本文组织为：第2节讨论无参数群算法（PSA），第3节定义旅行推销员问题，第4节给出无参数算法的分析方法，第5节总结工作。

二、无参数群算法

进化算法以参数为特征，这些参数可分为定性和定量参数[13]。定量参数大多是数字，定性参数用符号表示。参数可以根据控制策略的要求改变运行时间，也可以固定在单个值[13]。在进化算法中，如表1所述，存在广泛的可调谐参数。

Harik和Lobo于1999年首次设计了无参数遗传算法[14]。该方法取代了标准方法，标准方法除了选择适当的编码和运算符外，还需要尝试和错误方法来选择参数。无参数遗传算法使用户无需调整或猜测参数。定义的Harik Lobo无参数遗传算法的其他扩展版本是扩展紧凑遗传算法[15]和分层贝叶斯优化算法[16]。

De Jong[17]于1975年首次运行了遗传算法（GA），其功能很少，最终达到了50-100人的标准设置。在运行该算法时使用了0.6的交叉概率和0.001的突变概率。GA的此设置已在大多数应用程序中用作初步值集。在遗传算法中，文献表明大多数研究都集中在交叉率和突变率上。人口规模的调整很少得到解决。

参数调整可以通过适当分析每个参数在进化过程中的重要性来实现。Harik和Lobo[14]使GA无参数化的标准过程是分两步消除这些参数。第一步是交叉概率和选择率的阐述，然后是种群大小的阐述。在三个测试用例上的工作[14]的结果得出结论，交叉概率为0.5，选择率为4，符合模式定理。在这项工作中，参数调整被设计为动态改变。

三、 旅行商问题

离散优化是一组在约束和优化中使用离散变量的问题[18]。它可以由一个元组（S，f）来指定。集合S是满足特定限制的解的有限集合或可数集合。该函数将解集映射到实数集R。一些标准的离散优化问题是结构近似[19]、桥梁维护[20]、背包问题[21]、旅行推销员问题[22]、超立方体问题等等。进化算法专门适用于连续优化问题。离散化优化可以在离散化过程之后应用EA。采用Sigmoid函数、随机键、最小位置值、修正位置方程、大值优先级和最近整数等方法对连续问题进行离散化。

旅行推销员问题（TSP）[22]定义于1956年，在过去几十年中一直是一个标准的有限集问题。这个问题涉及到一个城市群和城市之间的距离。TSP算法的任务是找到涉及所有城市的最短路径，并在此过程中只到达一个城市一次。如果涉及5个或5个以下的城市，但涉及大量城市，这是一个简单的问题。它已被用作计算方法设计以及物流、规划和设计等应用中的基准问题。旅行推销员问题已应用于遗传算法[24]、差分进化[25]、萤火虫算法[26]和粒子群优化[27]。

三、PSA-PSO算法分析

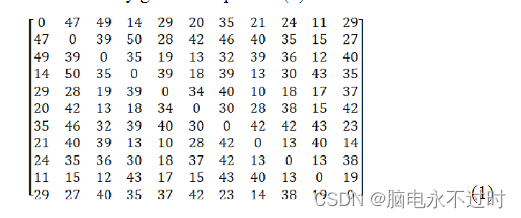
分析是通过一个定义为11个城市的旅行推销员问题进行的。城市之间的距离是在矩阵（1）中随机选择的。

评估是通过对不同的最大迭代和种群大小运行问题来完成的。评估是通过python编码完成的。该程序以初始c1=0.5，c1=1运行，维度数为11，由城市数给定。随机值范围已固定为[10，51]。PSA-PSO通过从最大迭代和种群大小的初始固定值开始运行。从执行结果来看，算法试图转向更好的结果。

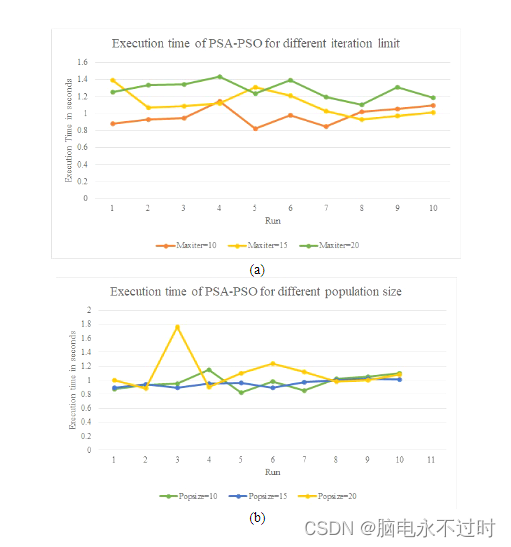
图5：无参数群算法PSO在以下参数方面的比较分析：（a）最大迭代极限（b）种群大小

图6给出了所提出的PSA-PSO的收敛性。可以看出，该算法在4次迭代内达到良好的收敛性，效果更好。将所提出的方法的性能与现有的无参数算法进行了比较：无参数单变量边际分布算法（P-UMDA）[29]、无参数扩展紧凑遗传算法（P-ECGA）[30]、无参数分层贝叶斯优化算法（P-HBOA）[31]和无参数进化投资组合（PEP）[1]。

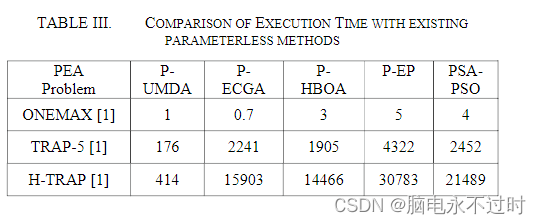
用于验证所提出的方法和现有方法的价值的问题是Onemax、级联陷阱-5（Trap-5）和层次陷阱一（H-Trap），如表3所示。所有的算法都在运行，直到达到全局最优。分析得出的结论是，当考虑执行时间时，无参数PSO比P-HBOA工作得更好。

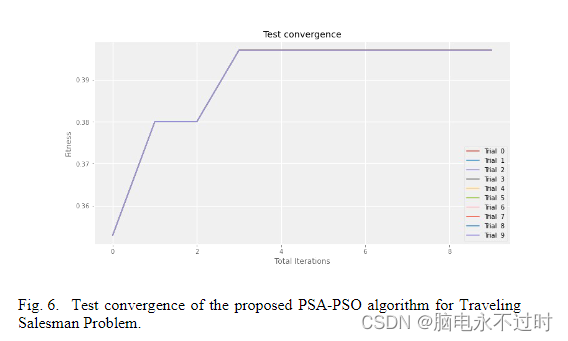
图6：测试所提出的PSA-PSO算法对旅行推销员问题的收敛性

V.结论

无参数群算法是选择进化参数的另一种选择。在这项工作中，我们提出了一种运行时方法来更改参数。该算法已被发现适用于旅行推销员问题。相同的算法可以扩展到其他离散优化问题。针对旅行商问题，设计并分析了无参数粒子群算法。