图像匹配简介
引用:深度学习应用在图像匹配的效果如何?
0、简介
图像匹配时后续高级图像处理的关键,近年来众多学者提出了许多优秀的方法,比如基于深度学习的特征点匹配算法、实时匹配算法、3D点云匹配算法、共面线点不变量匹配算法、以及基于深度学习的图像区域匹配等。
我们将各种图像匹配方法分为局部不变特征点匹配、直线匹配、区域匹配三类,介绍其优缺点和适用场景,利用DTU和Graf数据集来对各种方法进行比较。
1、局部不变特征点匹配
局部不变特征点匹配是发展最早的,一幅图像的特征点由关键点和描述子组成。关键点是特征点(在图像中的)位置、方向、尺度等信息;描述子通常是一个向量,描述关键点邻域的像素信息。在特征匹配时,通常只需要在向量空间对两个描述子进行比较,距离相近则判定为同一个特征点。
特征点从名字可以看出,选择的点具有一些特别的特征,所以一开始时角点、边缘点都可以作为潜在的特征点。
角点检测算法中最常用的是基于图像灰度的方法,如下图是角点检测。

1.1、Harris
Harris角点检测原理详解
思维之际-Harris角点
1.1.1、基本原理
该算法通过两个正交方向上强度的变化率对角点进行定义。
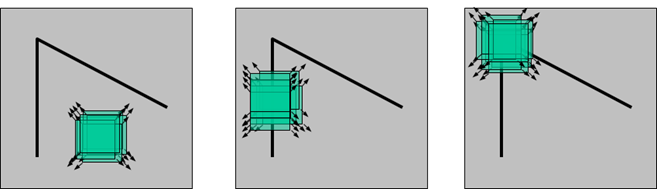
如上图,假设我们每次只能看到绿色方框大小的面积,那么我们通过绿色方块遍历整个图像来检测角点会发生以下几种情况:
- 1、当某次区域灰度变化较小时,认为该绿色区域没有角点(如左图),在X、Y方向上梯度(变化)较小。
- 2、当某次在一个方向上移动时,灰度发生了较大变化,而另一个方向移动时灰度变化较小,则该区域可能是一条直线(如中图),在X、Y方向的梯度上一个较大,一个较小。
- 3、当某次在任意方向上移动时,灰度都发送了变化,则该区域可能存在角点(如右图),在X、Y方向上的梯度都很大。
推理总结:
- 首先给出点和附近点的自相关函数,表示该点和周围点的关系,其值越小证明点到该附近点的方向上灰度值变化平缓;反之灰度值变化激烈;
- 对附近点的表示进行一阶近似,方便化简
- 化简后带入自相关函数,得到矩阵MMM
- 矩阵MMM的特征值λ1λ_1λ1,λ2λ_2λ2和自相关函数值:
| 类别 | 特征值关系 | 自相关函数值 |
|---|---|---|
| 平面 | 两个特征值都小,且近似相等 | 自相关函数值在各方面都小 |
| 直线 | 特征值一大一小 | 自相关函数值在某方向上大,其他方向小 |
| 角点 | 两个特征值都大,且近似相等 | 自相关函数在所有方向都大 |
1.1.2、算法实现
-
计算梯度
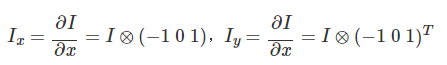
Ix=I(x+1,y)−I(x−1,y),Iy=I(x,y+1)−I(x,y−1)I_x=I(x+1,y)-I(x-1,y),I_y=I(x,y+1)-I(x,y-1)Ix=I(x+1,y)−I(x−1,y),Iy=I(x,y+1)−I(x,y−1) -
计算梯度乘积
Ix2=Ix∗IxI_x^2=I_x*I_xIx2=Ix∗Ix
Iy2=Iy∗IyI_y^2=I_y*I_yIy2=Iy∗Iy
Ixy=Ix∗IyI_{xy}=I_x*I_yIxy=Ix∗Iy -
高斯加权
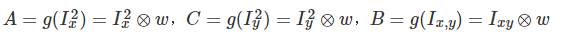
考虑到周围的梯度也能帮助判断角点,所以中心点梯度=中心点梯度*高斯权重
M:
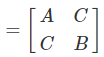
-
应当计算M的特征值,但实际没有计算特征值,而是曲线救国求响应值R
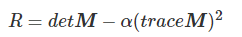
detM:表示矩阵M的行列式
trace:迹
α:经验常数,一般为0.04~0.06
然后将小于阈值t的R置零:
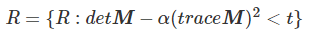
特征值与R的隐含关系:
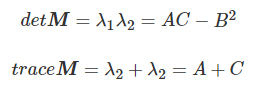
所以说变相计算了特征值 -
数据剔除
比如out[R >= np.max(R) * th] = [255, 0, 0]认为大于R最大值的0.1倍的才算是角点,将其标记位[255,0,0]用于展示
1.2、FAST
1.2.1、基本原理
- 现在判断像素p是不是一个角点,首先将p的像素值用III表示
- 设定一个阈值t
- 以像素p为中心,半径为3得到一个圆,该圆边界上有16个像素

- 如果这16个像素有n个连续的像素点,都比I+tI+tI+t大或者比I−t小I-t小I−t小,那么它就是一个角点。
实际上也容易理解,如果是一个角点,那么一半偏亮一半偏暗,所以是连续都比I+tI+tI+t大或者比I−t小I-t小I−t小。试想如果是平面,可能周围16个像素点比中心像素值高低都有,但是连续高或低的概率是很小的。
如何加快?
如果每次都检查16个像素点和中心像素点的大小关系,速度不够理想,所以有办法加快:该方法仅仅检查在位置1,9,5和13四个位置的像素,首先检测位置1和位置9,如果它们都比阈值暗或比阈值亮,再检测位置5和位置13。
1.2.2、优缺点
速度快,可用于实时性要求高的场合。但是FAST仅处理单一尺度图像,且孤立的噪点也容易被检测出来,当图像早点较多时会产生外点,鲁棒性下降
1.3、SIFT
SIFT算法原理
Sift中尺度空间、高斯金字塔、差分金字塔(DOG金字塔)、图像金字塔
Sift算子特征点提取、描述及匹配全流程解析
SIFT
SIFT即尺度不变特征变换,具有尺度不变性,是一种局部特征描述子。
1.3.1 前置知识:高斯金字塔和HOG金字塔
高斯金字塔

(注意这里的同尺寸的是一组图像,一组图像里面有很多层)
HOG金字塔
DOG(Difference of Gaussian),于是便很好理解了。
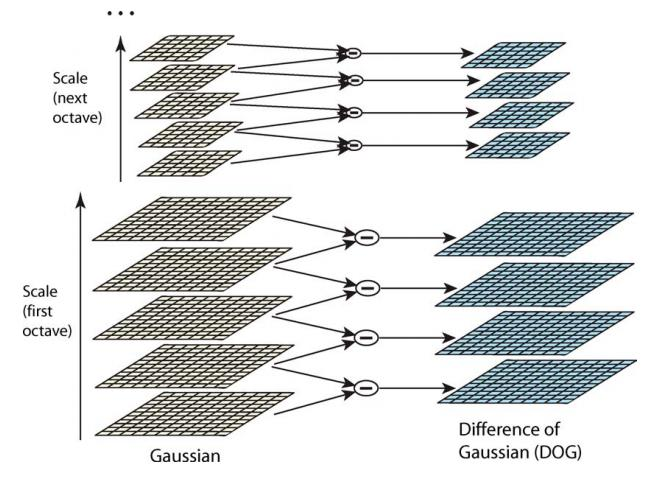
左边是高斯金字塔,每组的不同层之间做差,便得到了DOG金字塔。
归一化后的DOG金字塔图像,这些特征正是SIFT所要提取的“稳定”特征[DOG金字塔是高频信息,它包括了各种特征点以及边界噪点等,所以后面在搜寻关键点时会有筛掉边界点噪点的步骤]
1.3.2 原理
-
空间极值点检测(关键点的初步探查)
假设你现在得到了DOG金字塔,现在来判断一个像素点是不是极值点:1)先和自己的邻域像素点比较,比如和周围3x3的8个像素点比较;2)在和同组内尺寸相同,模糊程度不同)上层和下层图像的邻域比较,比如和上层同位置的9个点(3x3)比较,再和下层同位置的9个点比较,总共比较3*3*2=18个点.
这样保证了在尺度空间和邻域上都是极值点。一个点如果在DOG尺度空间本层以及上下两层的26个领域中是最大或最小值时,就认为该点是图像在该尺度下的一个特征点。 -
特征点的精确定位
因为诸如噪声等在DOG中也会出现,即对噪声和边缘等敏感,所以要将上步初步检测的关键点进行筛选。
这里如何实现的很多博客都没写明白,emmm…
(对DOG函数求导是得到梯度,看梯度得到周围的关系,根据周围的关系来判断是不是合格的?)
经过这一步,图中仅保留真正的特征点。
经典的图像匹配算法----SIFT
