js动态规划算法入门级教程,简单易懂

什么是动态规划?
以下为百度百科的定义:
动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。
我看过很多对动态规划的解释,大多数都说与分治法相似,都是分而治之的思想,将大问题分解成一个一个子问题,先去求子问题的解,当子问题求解后,大问题也就迎刃而解。
动态规划与分治法的不同:
动态规划求解的问题,经分解得到子问题往往是相互关联的。即下一个子问题的解是建立在上一个子问题求解的基础上。就比如求值5,5=2+3,想要求的5的解,先要知道2的解与3的解,即2与3是怎么得来的,即 2=1+1; 3=1+2 递推而来,有了2与3才能求出5。
接下来,我们使用 斐波那契数列 来举例说明。
什么是斐波那契数列?
斐波那契数列(Fibonacci sequence),又称黄金分割数列。斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*);这个数列从第三项开始,每一项都等于前两项之和。
1、递归解法
斐波那契数列的解法想必大家都知道,最简单粗暴的解法就是递归。
function fib(n){if ( n < 2) return n; // 边界条件 F(0)=0,F(1)=1return fib(n-1) + fib(n-2);
}
let result = fib(10);
console.log(result); // 55
虽然使用递归的方式简单易懂,但是却不推荐这种做法,因为对于性能消耗太大,当数量级增长到一定程度时,前端会直接卡爆浏览器,后端的话或许会直接让服务器宕机。而且使用递归的方式,渐进时间复杂度为 O(2ⁿ),指数级在时间复杂度的量级中非常高,如果能优化,绝对要优化。
时间复杂度 由简单到复杂:
| n | O(1) 常数阶 | O(logn) 对数阶 | O(n) 线性阶 | O(nlogn) 线性对数阶 | O(n²) 平方阶 | O(n³) 立方阶 | O(2ⁿ) 指数阶 | O(n!) 阶乘阶 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 2 | 1 |
| 2 | 1 | 1 | 2 | 2 | 4 | 8 | 4 | 2 |
| 4 | 1 | 2 | 4 | 8 | 16 | 64 | 16 | 24 |
| 8 | 1 | 3 | 8 | 24 | 64 | 512 | 256 | 40320 |
| 16 | 1 | 4 | 16 | 64 | 256 | 4096 | 65536 | 2.0923E+13 |
| 32 | 1 | 5 | 32 | 160 | 1024 | 32768 | 4.295E+09 | 2.6313E+35 |
2、动态规划解法
使用递归的解法会有许多重复的子项被计算,以求 fib(10) 为例,如下图:
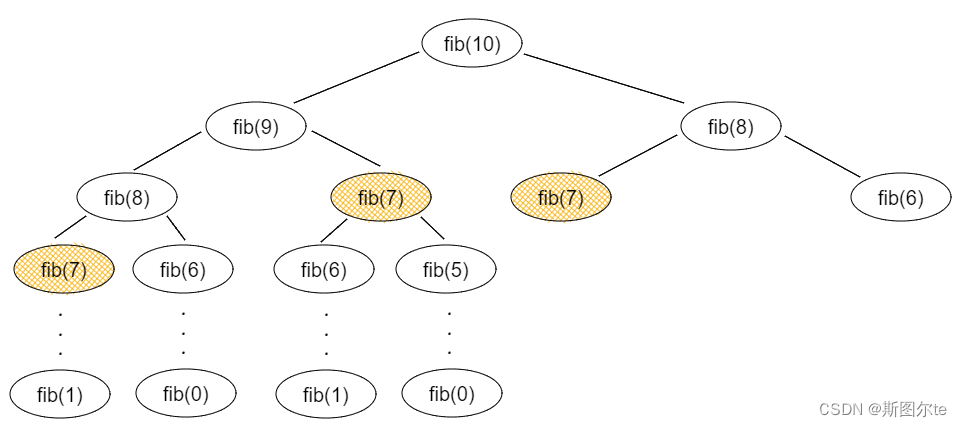
递归会将之前已经计算过的子项在其他子项中重新计算,如上面的 fib(7),fib(7) 里面的所有子项也会被一层一层重新计算,这就是递归为什么损耗性能。既然已经计算过了,为什么我们不能在计算第一遍的时候直接存储,再次遇到直接拿来用呢?还要去计算一遍,你说傻不傻。
这时候 动态规划 的思想就用上了,动态规划是自底向上的,而递归是自上而下的。
那如何自底向上呢?
我们知道 F(0)=0、F(1)=1;定义一个数组,里面已经存在两项 let arr = [0, 1];这时候我们可以求出第3项的值为arr[2]=arr[0]+arr[1];最后数组的结果为 arr = [0, 1, 1],这时候有了第2项与第3项的结果,我们又可以求出第4项的结果;如此循环,直到求出最终结果。
动态规划代码:
function fib(n) {const arr = [0, 1];// 索引从0开始,i=2时求第3项的值。 求F(n),要计算n;所以要 i<=nfor (let i = 2; i <= n; i++){arr[i] = arr[i-1] + arr[i-2];}// 打印 F(10)数列console.log(arr); // [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]return arr[arr.length-1];
}
let result = fib(10);
console.log(result); // 55
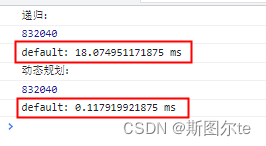
动态规划的 斐波那契数列 的时间复杂度为 O(n);比递归的 O(2ⁿ) 不知道强了多少倍!我们可以使用 console.time() 以及 console.timeEnd() 来计算一下两段程序所耗时间:
console.time();
console.log("递归:")
function fib(n){if ( n < 2) return n;return fib(n-1) + fib(n-2);
}
let result = fib(30);
console.log(result);
console.timeEnd();console.time();
console.log("动态规划:")
function fibDP(n) {const arr = [0, 1];for (let i = 2; i <= n; i++){arr[i] = arr[i-1] + arr[i-2];}return arr[arr.length-1];
}
let resultDP = fibDP(30);
console.log(resultDP);
console.timeEnd();