JavaScript【图论】
目录
1.图的简介
1.什么是图?
2.图的特点:
3.2.图的表示图的常用术语:
2.图的表示
方法一:邻接矩阵
如上图所示:
邻接矩阵的问题:
方法二:邻接表
如上图所示:
邻接表的问题:
3.封装图结构
1.添加字典类和队列类
2.创建图类
3.添加顶点和边
如图所示:
代码实现:
4.转换为字符串输出
代码实现:
测试代码:
测试结果
5.图的遍历
图的遍历思想
遍历图的两种算法:
编辑
顶点状态表示
4.广度优先搜索【队列实现】
算法的思路:
实现思路:
代码实现:
过程详解:
测试代码:
5.深度优先搜索【栈实现】
算法的思路:
实现思路:
在dfs方法中:
在dfsVisit方法中:
代码实现:
过程详解:
测试代码:
测试结果:
6.完整代码
1.图的简介
1.什么是图?
- 图结构是一种与树结构有些相似的数据结构;
- 图论是数学的一个分支,并且,在数学中,树是图的一种;
- 图论以图为研究对象,研究顶点和边组成的图形的数学理论和方法;
- 主要的研究目的为:事物之间的联系,顶点代表事物,边代表两个事物间的关系;
2.图的特点:
- 一组顶点:通常用 V (Vertex)表示顶点的集合;
- 一组边:通常用 E (Edge)表示边的集合;
- 边是顶点和顶点之间的连线;
- 边可以是有向的,也可以是无向的。比如A----B表示无向,A ---> B 表示有向;
3.2.图的表示图的常用术语:
顶点:表示图中的一个节点;
边:表示顶点和顶点给之间的连线;
相邻顶点:由一条边连接在一起的顶点称为相邻顶点;
度:一个顶点的度是相邻顶点的数量;
路径:
- 简单路径:简单路径要求不包含重复的顶点;
- 回路:第一个顶点和最后一个顶点相同的路径称为回路;
无向图:图中的所有边都是没有方向的;
有向图:图中的所有边都是有方向的;
无权图:无权图中的边没有任何权重意义;
带权图:带权图中的边有一定的权重含义;
2.图的表示

方法一:邻接矩阵
表示图的常用方式为:邻接矩阵。
可以使用二维数组来表示邻接矩阵;
邻接矩阵让每个节点和一个整数相关联,该整数作为数组的下标值;【二维数组】
使用一个二维数组来表示顶点之间的连接;
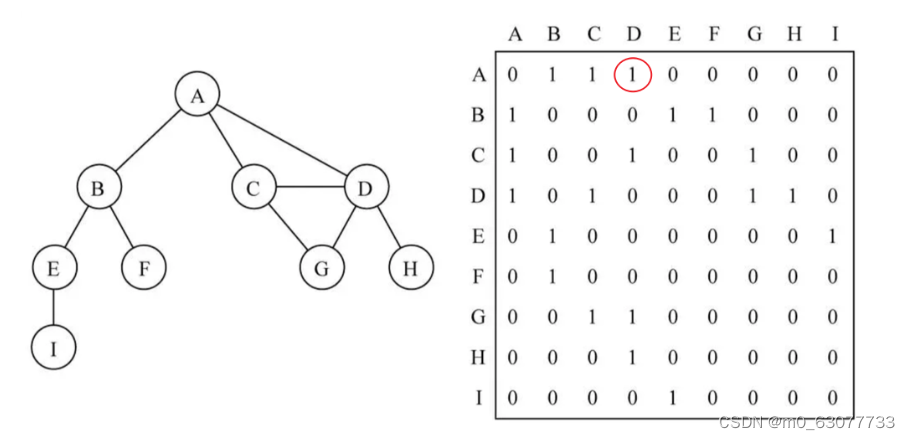
如上图所示:
- 二维数组中的0表示没有连线,1表示有连线;
- 如:A[ 0 ] [ 3 ] = 1,表示 A 和 D 之间有连接;A[行][列]
- 邻接矩阵的对角线上的值都为0,表示A - A ,B - B,等自回路都没有连接(自己与自己之间没有连接);
- 若为无向图,则邻接矩阵应为对角线上元素全为0的对称矩阵;
邻接矩阵的问题:
- 如果图是一个稀疏图,那么邻接矩阵中将存在大量的 0,造成存储空间的浪费;
方法二:邻接表
- 邻接表由图中每个顶点以及和顶点相邻的顶点列表组成;
- 这个列表可用多种方式存储,比如:数组/链表/字典(哈希表)等都可以;
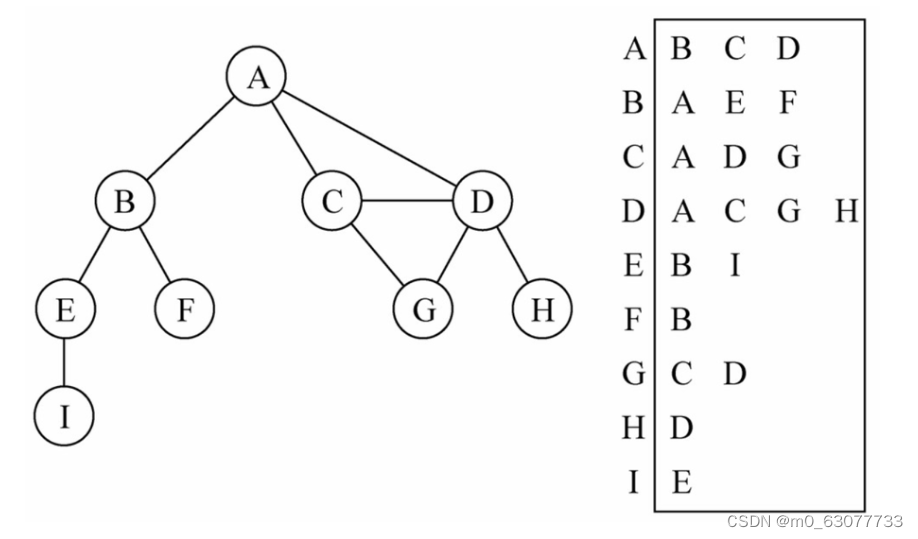
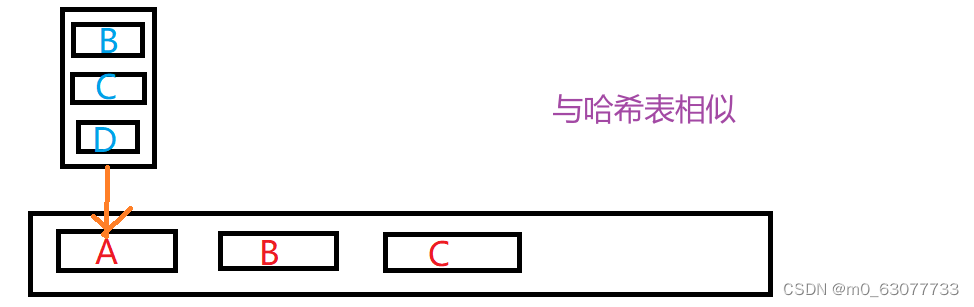
如上图所示:
- 图中可清楚看到A与B、C、D相邻,假如要表示这些与A顶点相邻的顶点(边),可以通过将它们作为A的值(value)存入到对应的数组/链表/字典中。
- 之后,通过键(key)A可以十分方便地取出对应的数据;
邻接表的问题:
- 邻接表可以简单地得出出度,即某一顶点指向其他顶点的个数;
- 但是,邻接表计算入度(指向某一顶点的其他顶点的个数称为该顶点的入度)十分困难。此时需要构造逆邻接表才能有效计算入度;
3.封装图结构
在实现过程中采用邻接表的方式来表示边,使用字典类来存储邻接表
1.添加字典类和队列类
首先需要引入之前实现的,之后会用到的字典类和队列类:
//封装字典类
function Dictionary(){//字典属性this.items = {}//字典操作方法//一.在字典中添加键值对Dictionary.prototype.set = function(key, value){this.items[key] = value}//二.判断字典中是否有某个keyDictionary.prototype.has = function(key){return this.items.hasOwnProperty(key)}//三.从字典中移除元素Dictionary.prototype.remove = function(key){//1.判断字典中是否有这个keyif(!this.has(key)) return false//2.从字典中删除keydelete this.items[key]return true}//四.根据key获取valueDictionary.prototype.get = function(key){return this.has(key) ? this.items[key] : undefined}//五.获取所有keysDictionary.prototype.keys = function(){return Object.keys(this.items)}//六.size方法Dictionary.prototype.keys = function(){return this.keys().length}//七.clear方法Dictionary.prototype.clear = function(){this.items = {}}
}// 基于数组封装队列类function Queue() {// 属性this.items = []// 方法// 1.将元素加入到队列中Queue.prototype.enqueue = element => {this.items.push(element)}// 2.从队列中删除前端元素Queue.prototype.dequeue = () => {return this.items.shift()}// 3.查看前端的元素Queue.prototype.front = () => {return this.items[0]}// 4.查看队列是否为空Queue.prototype.isEmpty = () => {return this.items.length == 0;}// 5.查看队列中元素的个数Queue.prototype.size = () => {return this.items.length}// 6.toString方法Queue.prototype.toString = () => {let resultString = ''for (let i of this.items){resultString += i + ' '}return resultString}}
2.创建图类
先创建图类Graph,并添加基本属性,再实现图类的常用方法:
//封装图类function Graph (){//属性:顶点(数组)/边(字典)this.vertexes = [] //顶点this.edges = new Dictionary() //边}
3.添加顶点和边
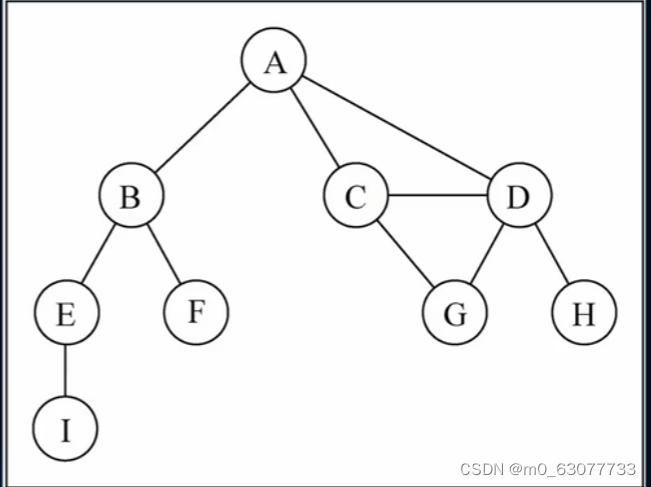
如图所示:
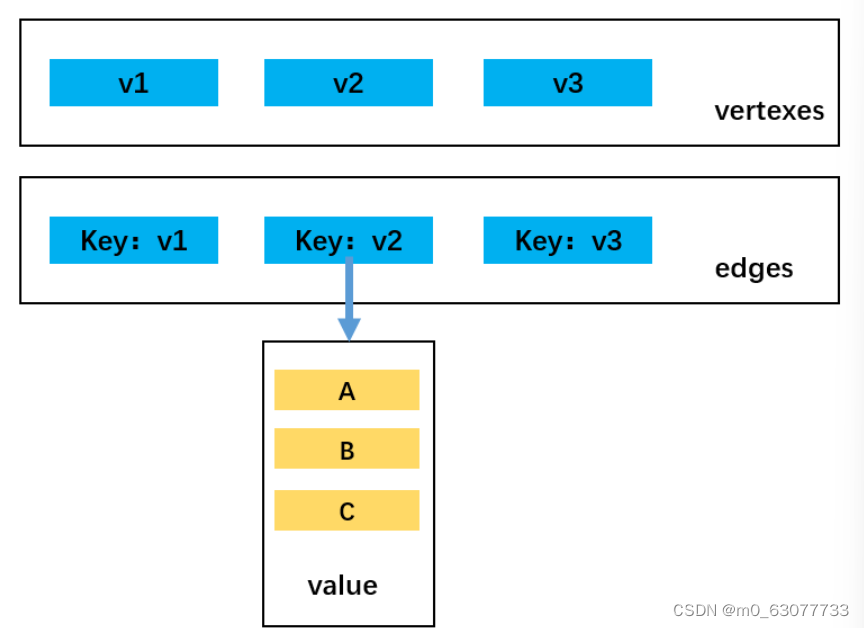
创建一个数组对象vertexes存储图的顶点;创建一个字典对象edges存储图的边,其中key为顶点,value为存储key顶点相邻顶点的数组。
代码实现:
//1.添加顶点的方法// v:表示顶点Graph.prototype.addVertex=function(v){// 因为使用数值存储,所以使用pushthis.vertexes.push(v)// set:在字典中添加键值对this.edges.set(v,[])}// 2.添加边的方法Graph.prototype.addEdge=function(v1,v2){// get:根据key获取value// push:将v2加入到v1的数组中//取出字典对象edges中存储边的数组,并添加关联顶点this.edges.get(v1).push(v2)//表示的是无向表,故要添加互相指向的两条边this.edges.get(v2).push(v1)}4.转换为字符串输出
为图类Graph添加toString方法,实现以邻接表的形式输出图中各顶点。
代码实现:
// 修改toString方法Graph.prototype.toString = function () {// 1.定义字符串,保存最终的结果var resultString = ""// 2.遍历所有的顶点for (var i = 0; i < this.vertexes.length; i++) {resultString += this.vertexes[i] + '->'// 取出顶点对应的边var vEdges = this.edges.get(this.vertexes[i])for (var j = 0; j < vEdges.length; j++) {resultString += vEdges[j] + ' '}resultString += '\n'}return resultString}测试代码:
//测试代码//1.创建图结构let graph = new Graph()//2.添加顶点let myVertexes = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']for (let i = 0; i < myVertexes.length; i++) {graph.addVertex(myVertexes[i])}//3.添加边graph.addEdge('A', 'B')graph.addEdge('A', 'C')graph.addEdge('A', 'D')graph.addEdge('C', 'D')graph.addEdge('C', 'G')graph.addEdge('D', 'G')graph.addEdge('D', 'H')graph.addEdge('B', 'E')graph.addEdge('B', 'F')graph.addEdge('E', 'I')//4.输出结果console.log(graph.toString());测试结果

5.图的遍历
图的遍历思想
- 图的遍历思想与树的遍历思想一样,意味着需要将图中所有的顶点都访问一遍,并且不能有重复的访问(上面的toString方法会重复访问);
遍历图的两种算法:
- 广度优先搜索(Breadth - First Search,简称BFS);===>【逐步查看邻边】
- 深度优先搜索(Depth - First Search,简称DFS);===>【一黑到底】
- 两种遍历算法都需要指定第一个被访问的顶点;
顶点状态表示
为了记录顶点是否被访问过,使用三种颜色来表示它们的状态
- 白色:表示该顶点还没有被访问过;
- 灰色:表示该顶点被访问过,但其相邻顶点并未完全被访问过(与该顶点相连的其他顶点);
- 黑色:表示该顶点被访问过,且其所有相邻顶点都被访问过;
首先封装initializeColor方法将图中的所有顶点初始化为白色,代码实现如下:
//初始化状态颜色Graph.prototype.initializeColor = function(){let colors = []for (let i = 0; i < this.vertexes.length; i++) {colors[this.vertexes[i]] = 'white';}return colors}
4.广度优先搜索【队列实现】
算法的思路:
- 广度优先搜索算法会从指定的第一个顶点开始遍历图,先访问其所有的相邻顶点,就像一次访问图的一层;
- 也可以说是先宽后深地遍历图中的各个顶点;
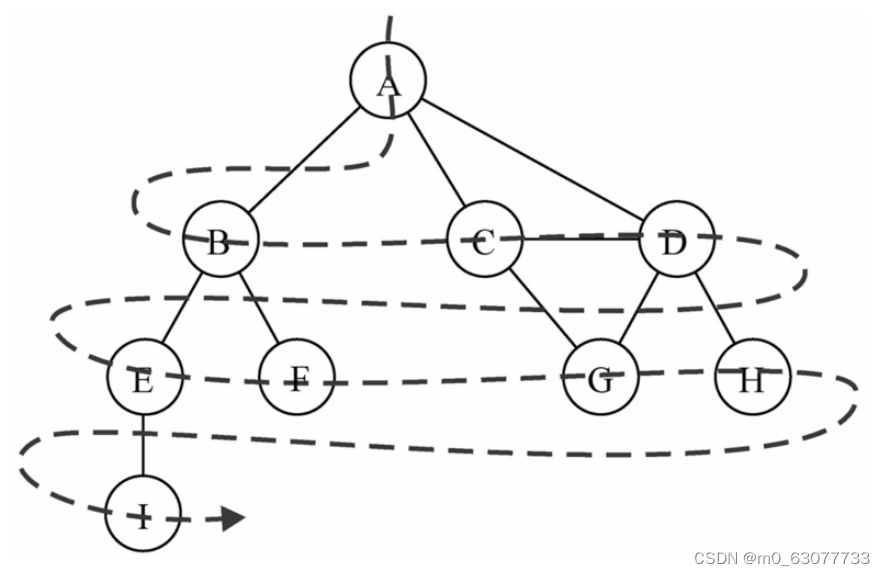
实现思路:
基于队列可以简单地实现广度优先搜索算法:
- 首先创建一个队列Q(尾部进,首部出);
- 调用封装的initializeColor方法将所有顶点初始化为白色;
- 指定第一个顶点A,将A标注为灰色(被访问过的节点),并将A放入队列Q中;
- 循环遍历队列中的元素,只要队列Q非空,就执行以下操作:
- 先将灰色的A从Q的首部取出;
- 取出A后,将A的所有未被访问过(白色)的相邻顶点依次从队列Q的尾部加入队列,并变为灰色。以此保证,灰色的相邻顶点不重复加入队列;
- A的全部相邻节点加入Q后,A变为黑色,在下一次循环中被移除Q外;
代码实现:
//初始化状态颜色
Graph.prototype.initializeColor = function () {let colors = []for (let i = 0; i < this.vertexes.length; i++) {colors[this.vertexes[i]] = 'white';}return colors
}// 实现广度优先搜索(BFS)
Graph.prototype.bfs=function(initV,handler){// 1.初始化颜色var color=this.initializeColor()// 2.创建队列var queue=new Queue()// 3.将顶点加入到队列中queue.enqueue(initV)// 4.循环从队列中取出元素while(!queue.isEmpty()){// 4.1 从队列中取出一个顶点var v=queue.dequeue()// 4.2 获取和顶点相连的另外顶点var vList=this.edges.get(v)// 4.3将v的颜色设置为灰色colors[v]='gray'// 4.4遍历所有的顶点,并且加入队列中for (let i = 0; i < vList.length; i++) {const a = vList[i];//判断相邻顶点是否被探测过,被探测过则不加入队列中;并且加入队列后变为灰色,表示被探测过if (colors[a] == 'white') {colors[a] = 'gray'queue.enqueue(a)}}// 4.5访问顶点handler(v)// 4.6 将顶点设置为黑色colors[v]='black'}
}过程详解:
下为指定的第一个顶点为A时的遍历过程:
- 如 a 图所示,将在字典edges中取出的与A相邻的且未被访问过的白色顶点B、C、D放入队列que中并变为灰色,随后将A变为黑色并移出队列;
- 接着,如图 b 所示,将在字典edges中取出的与B相邻的且未被访问过的白色顶点E、F放入队列que中并变为灰色,随后将B变为黑色并移出队列;
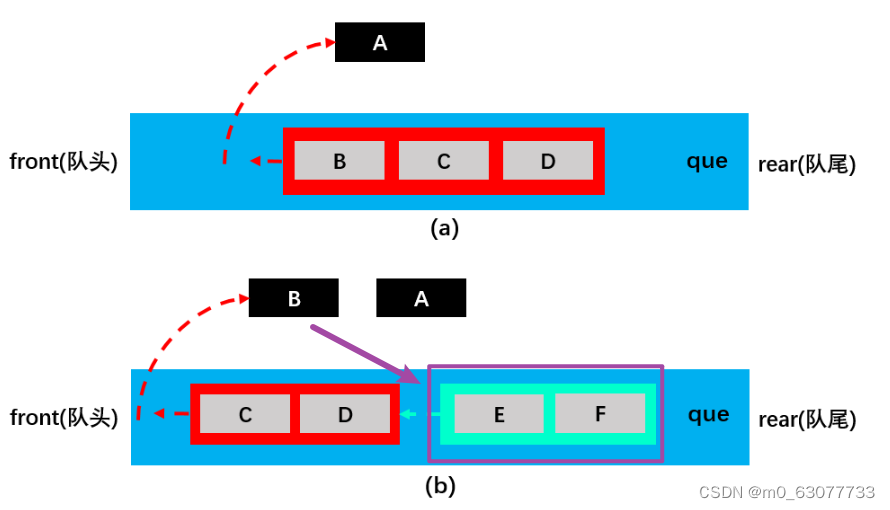
- 如 c 图所示,将在字典edges中取出的与C相邻的且未被访问过的白色顶点G(A,D也相邻不过已变为灰色,所以不加入队列)放入队列que中并变为灰色,随后将C变为黑色并移出队列;
- 接着,如图 d 所示,将在字典edges中取出的与D相邻的且未被访问过的白色顶点H放入队列que中并变为灰色,随后将D变为黑色并移出队列。
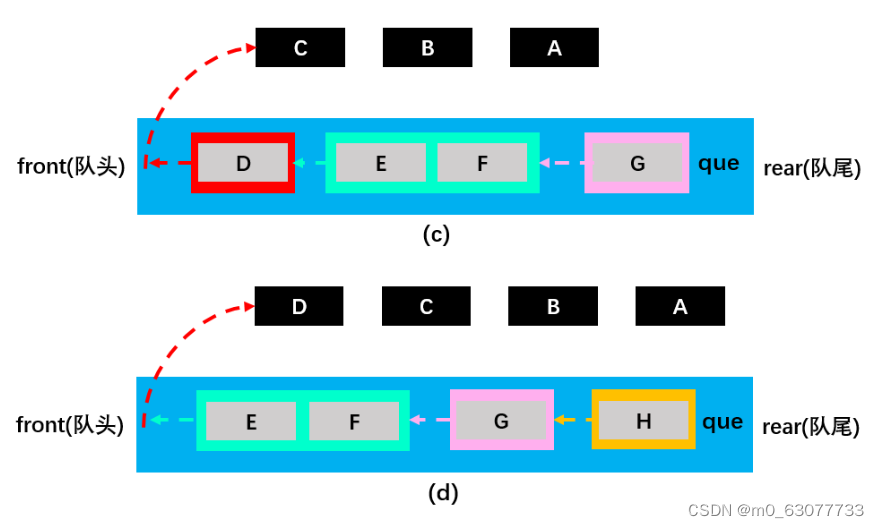
如此循环直到队列中元素为0,即所有顶点都变黑并移出队列后才停止,此时图中顶点已被全部遍历。
测试代码:
//测试代码//1.创建图结构let graph = new Graph()//2.添加顶点let myVertexes = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']for (let i = 0; i < myVertexes.length; i++) {graph.addVertex(myVertexes[i])}//3.添加边graph.addEdge('A', 'B')graph.addEdge('A', 'C')graph.addEdge('A', 'D')graph.addEdge('C', 'D')graph.addEdge('C', 'G')graph.addEdge('D', 'G')graph.addEdge('D', 'H')graph.addEdge('B', 'E')graph.addEdge('B', 'F')graph.addEdge('E', 'I')//4.测试bfs遍历方法let result = ""graph.bfs(graph.vertexes[0], function(v){result += v + "-"})console.log(result);
5.深度优先搜索【栈实现】
算法的思路:
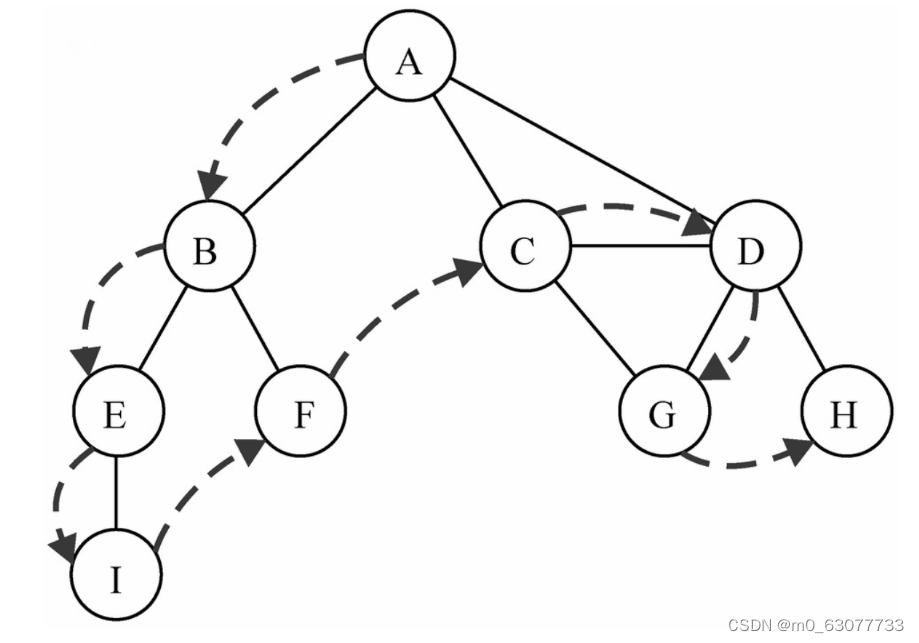
- 深度优先搜索算法将会从指定的第一个顶点开始遍历图,沿着一条路径遍历直到该路径的最后一个顶点都被访问过为止;
- 接着沿原来路径回退并探索下一条路径,即先深后宽地遍历图中的各个顶点;
实现思路:
- 可以使用栈结构来实现深度优先搜索算法;
- 深度优先搜索算法的遍历顺序与二叉搜索树中的先序遍历较为相似,同样可以使用递归来实现(递归的本质就是函数栈的调用)。
基于递归实现深度优先搜索算法:定义dfs方法用于调用递归方法dfsVisit,定义dfsVisit方法用于递归访问图中的各个顶点。
在dfs方法中:
- 首先,调用initializeColor方法将所有顶点初始化为白色;
- 然后,调用dfsVisit方法遍历图的顶点;
在dfsVisit方法中:
- 首先,将传入的指定节点v标注为灰色;
- 接着,处理顶点V;
- 然后,访问V的相邻顶点;
- 最后,将顶点v标注为黑色;
代码实现:
//初始化状态颜色
Graph.prototype.initializeColor = function () {let colors = []for (let i = 0; i < this.vertexes.length; i++) {colors[this.vertexes[i]] = 'white';}return colors
}// 深度优先搜索(DFS)
Graph.prototype.dfs=function(initV, handler) {// 1.初始化颜色var colors = this.initializeColor()// 2.从某一个顶点开始this.dfsVisit(initV, colors, handler)
}Graph.prototype.dfsVisit=function(v,colors,handler){// 1.将颜色设置为灰色colors[v]='gray'// 2.处理v顶点handler(v)// 3.访问v相连的顶点var vList=this.edges.get(v)for(var i=0;i过程详解:
这里主要解释一下代码中的第3步操作:访问指定顶点的相邻顶点。
- 以指定顶点A为例,先从储存顶点及其对应相邻顶点的字典对象edges中取出由顶点A的相邻顶点组成的数组:
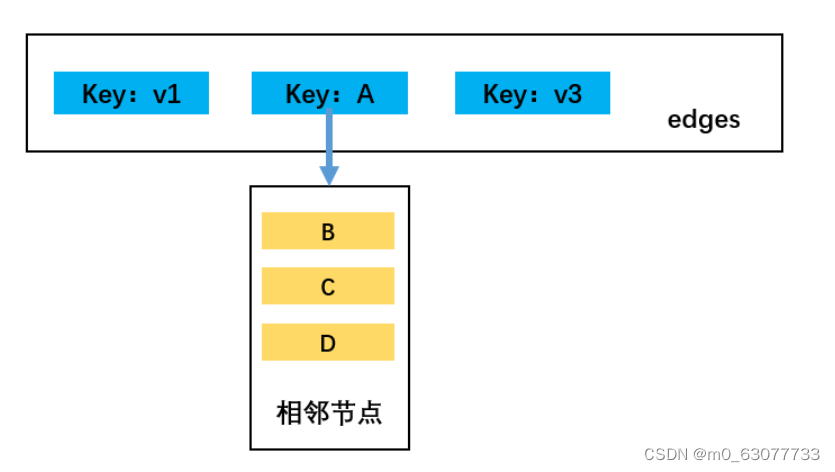
- 第一步:A顶点变为灰色,随后进入第一个for循环,遍历A白色的相邻顶点:B、C、D;在该for循环的第1次循环中(执行B),B顶点满足:colors == "white",触发递归,重新调用该方法;
- 第二步:B顶点变为灰色,随后进入第二个for循环,遍历B白色的相邻顶点:E、F;在该for循环的第1次循环中(执行E),E顶点满足:colors == "white",触发递归,重新调用该方法;
- 第三步:E顶点变为灰色,随后进入第三个for循环,遍历E白色的相邻顶点:I;在该for循环的第1次循环中(执行I),I顶点满足:colors == "white",触发递归,重新调用该方法;
- 第四步:I顶点变为灰色,随后进入第四个for循环,由于顶点I的相邻顶点E不满足:colors == "white",停止递归调用。过程如下图所示:
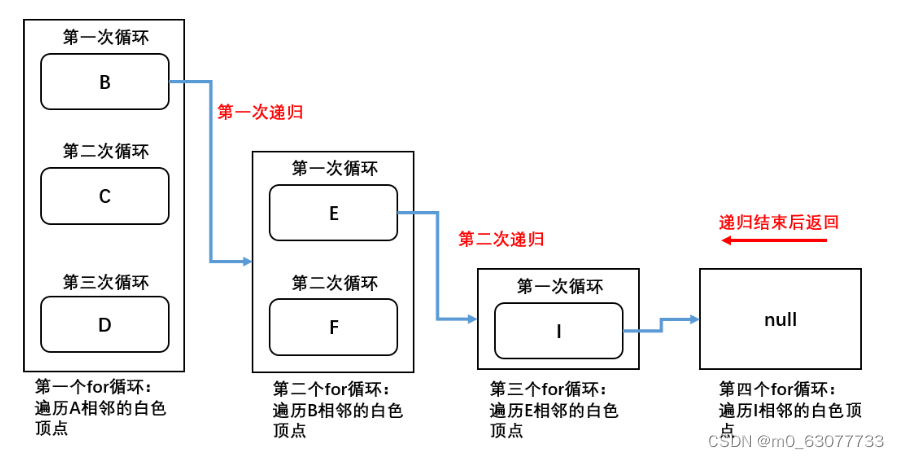
- 第五步:递归结束后一路向上返回,首先回到第三个for循环中继续执行其中的第2、3...次循环,每次循环的执行过程与上面的同理,直到递归再次结束后,再返回到第二个for循环中继续执行其中的第2、3...次循环....以此类推直到将图的所有顶点访问完为止。
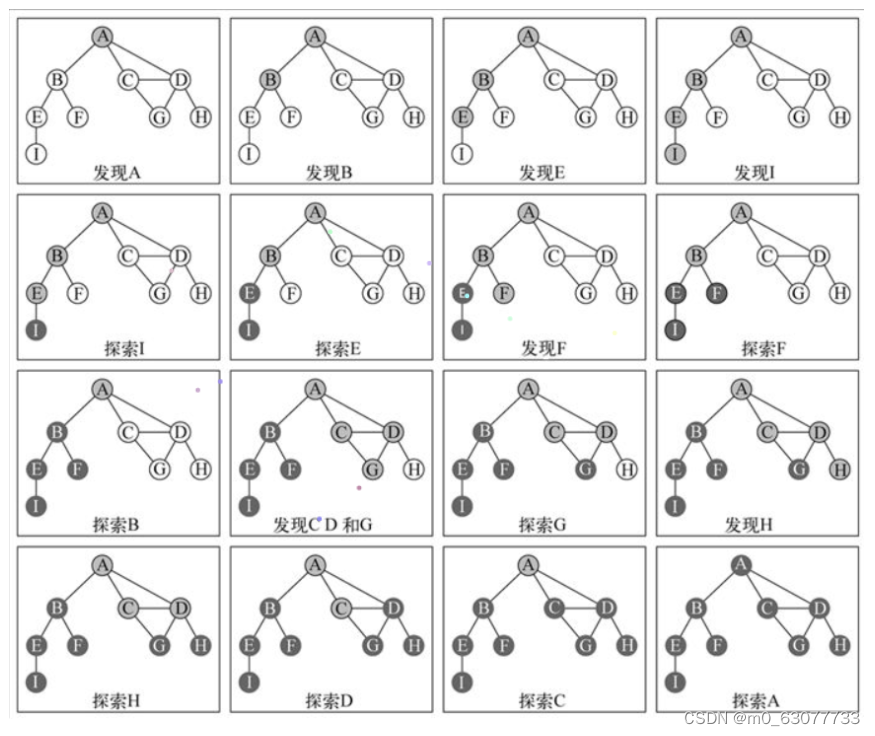
下图为遍历图中各顶点的完整过程:
- 发现表示访问了该顶点,状态变为灰色;
- 探索表示既访问了该顶点,也访问了该顶点的全部相邻顶点,状态变为黑色;
- 由于在顶点变为灰色后就调用了处理函数handler,所以handler方法的输出顺序为发现顶点的顺序即:A、B、E、I、F、C、D、G、H 。
测试代码:
//测试代码//1.创建图结构let graph = new Graph()//2.添加顶点let myVertexes = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']for (let i = 0; i < myVertexes.length; i++) {graph.addVertex(myVertexes[i])}//3.添加边graph.addEdge('A', 'B')graph.addEdge('A', 'C')graph.addEdge('A', 'D')graph.addEdge('C', 'D')graph.addEdge('C', 'G')graph.addEdge('D', 'G')graph.addEdge('D', 'H')graph.addEdge('B', 'E')graph.addEdge('B', 'F')graph.addEdge('E', 'I')//4.测试dfs遍历顶点let result = ""graph.dfs(graph.vertexes[0], function(v){result += v + "-"})console.log(result);测试结果:
6.完整代码
Document

