作者：非妃是公主
专栏：《计算机图形学》
博客地址：https://blog.csdn.net/myf_666
个性签：顺境不惰，逆境不馁，以心制境，万事可成。——曾国藩

文章目录

• 专栏推荐
• 专栏系列文章
• 序
• 一、算法原理
• 二、伪代码
• • 2.1 中点分割算法——伪代码
• 三、OpenGL代码实现
• 四、效果展示
• • 4.1 裁剪效果
  • 4.2 测试代码
• 五、梁友栋-Barsky算法
• the end……

专栏推荐

专栏系列文章

序

计算机图形学（英语：computer graphics，缩写为CG）是研究计算机在硬件和软件的帮助下创建计算机图形的科学学科，是计算机科学的一个分支领域，主要关注数字合成与操作视觉的图形内容。虽然这个词通常被认为是指三维图形，事实上同时包括了二维图形以及影像处理。

一、算法原理

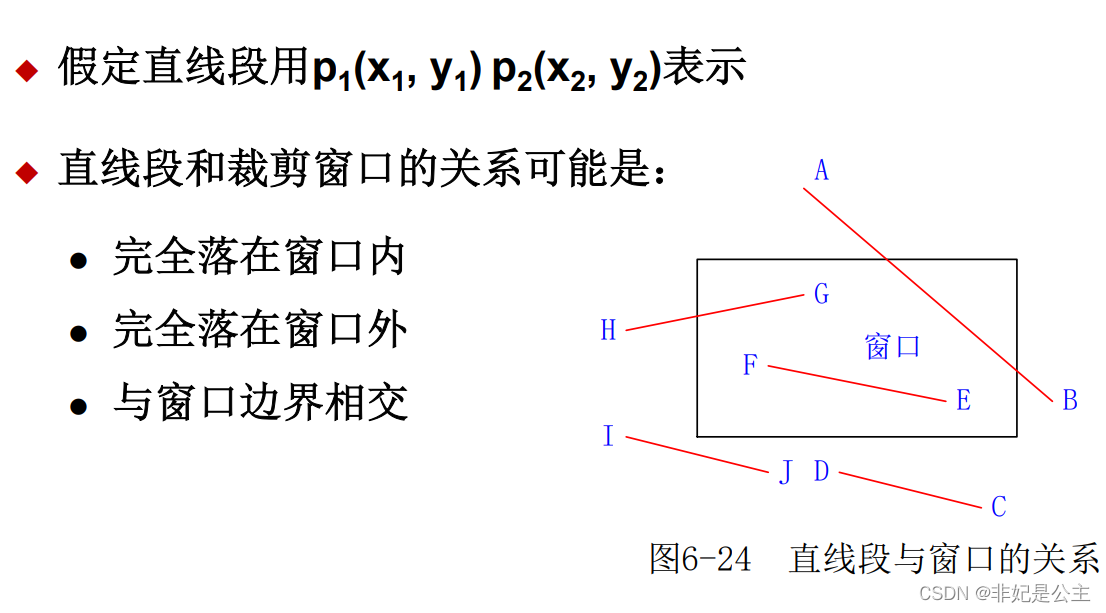
采用的方法是，对线段的两个端点进行编码，如下：

二、伪代码

① 输入直线段的两端点坐标：p1(x1,y1)、p2(x2,y2)，以及窗口的四条边界坐标：wyt、wyb、wxl和wxr。

② 对p1、p2进行编码：点p1的编码为code1，点p2的编码为code2。

③ 若code1|code2=0，简取之，转⑥；否则，若code1&code2≠0，简弃之，转⑦；当上述两条均不满足时，进行步骤④ 。

④ 确保p1在窗口外部：若p1在窗口内，则交换p1和p2的坐标值和编码。

⑤ 按左、右、下、上的顺序求出直线段与窗口边界的交点，并用该交点的坐标值替换p1的坐标值。去掉p1s这一段。转②。

⑥ 画当前的直线段p1p2。 ⑦算法结束。

由于在 ⑤ 的求解过程中，需要涉及到线段与窗口边界的交点，采用的方法是中点分割算法，它是一种二分法来不断逼近真实交点的求解方法，具体如下。

2.1 中点分割算法——伪代码

①若code1|code2=0，对直线段应简取之，结束；否则，若code1&code2≠0，对直线段可简弃之，结束；当这两条均不满足时，进行步骤② 。

②找出该直线段离窗口边界最远的点和该直线段的中点。判中点是否在窗口内：若不在，则把中点和离窗口边界最远点构成的线段丢掉，以线段上的另一点和该中点再构成线段求其中点；如中点在窗口内，则又以中点和最远点构成线段，并求其中点，直到中点接近窗口边界，则该中点就是该线段落在窗口内的一个端点坐标。

③如另一点在窗口内，则经②即确定了该线段在窗口内的部分。如另一点不在窗口内，则该点和所求出的在窗口上的那一点构成一条线段，重复步骤②，即可求出落在窗口内的另一点。

三、OpenGL代码实现

/// 

/// 对线段的端点进行编码
/// 
/// 待编码的点
/// 窗口的左边缘
/// 窗口的右边缘
/// 窗口的下边缘
/// 窗口的上边缘
/// 
int codePoint(VERTEX p1, int wxl, int wxr, int wyb, int wyt) {int codeP1;// 编码p1if (p1.x < wxl) {if (p1.y < wyb) {codeP1 = 5;}else if (p1.y < wyt) {codeP1 = 1;}else {codeP1 = 9;}}else if (p1.x < wxr) {if (p1.y < wyb) {codeP1 = 4;}else if (p1.y < wyt) {codeP1 = 0;}else {codeP1 = 8;}}else {if (p1.y < wyb) {codeP1 = 6;}else if (p1.y < wyt) {codeP1 = 2;}else {codeP1 = 10;}}return codeP1;
}// 中点Bresenham算法绘制直线段(k任意)
void  MidBhline2(int  x0, int  y0, int  x1, int  y1) {int  dx, dy, d, UpIncre, DownIncre, x, y;if (x0 > x1) {				// x0为起始点，x1为终止点x = x1; x1 = x0; x0 = x; y = y1; y1 = y0; y0 = y;}x = x0; y = y0; dx = x1 - x0; dy = y1 - y0;// 0 <= k <= 1if (dy >= 0 && dy < dx) {d = dx - 2 * dy;			// d的初始值UpIncre = 2 * dx - 2 * dy;	// 2dx*(1 + k)DownIncre = -2 * dy;		// 2dx(-k)glBegin(GL_POINTS);		// 开始绘制点while (x <= x1) {glVertex2i(x, y);		// 画点x++;					// 更新xif (d < 0) {			// 根据d的符号更新d和yy++;d += UpIncre;}elsed += DownIncre;}glEnd();					// 结束绘制点}// k > 1else if (dy >= 0 && dy > dx) {d = -dy + 2 * dx;			// d的初始值UpIncre = 2 * dx;			// 2dx*(1)DownIncre = 2 * dx - 2 * dy;// 2dx*(1-k)glBegin(GL_POINTS);		// 开始绘制点while (x <= x1) {glVertex2i(x, y);		// 画点y++;					// 更新yif (d < 0) {			// 根据d的符号更新d和xd += UpIncre;}else {x++;d += DownIncre;}}glEnd();}// -1 <= k < 0else if (dy < 0 && dy >= -dx) {d = -dx - 2 * dy;			// d的初始值UpIncre = -2 * dy;			// 2dx*(1)DownIncre = -2 * dx - 2 * dy;// 2dx*(1-k)glBegin(GL_POINTS);			// 开始绘制点while (x <= x1) {glVertex2i(x, y);		// 画点x++;					// 更新yif (d < 0) {			// 根据d的符号更新d和xd += UpIncre;}else {y--;d += DownIncre;}}glEnd();}// k < -1else if (dy < 0 && dy < -dx) {d = -2 * dx - dy;			// d的初始值UpIncre = -2 * dx - 2 * dy;	// 2dx*(1)DownIncre = -2 * dx;		// 2dx*(1-k)glBegin(GL_POINTS);			// 开始绘制点while (x <= x1) {glVertex2i(x, y);		// 画点y--;					// 更新yif (d < 0) {			// 根据d的符号更新d和xx++;d += UpIncre;}else {d += DownIncre;}}glEnd();}
}/// 

/// Cohen-Sutherland算法 编码裁剪直线段
/// 
/// 线段的起始点
/// 线段的终点
/// 窗口的左边缘
/// 窗口的右边缘
/// 窗口的下边缘
/// 窗口的上边缘
void cohenCropLine(VERTEX p1, VERTEX p2, int wxl, int wxr, int wyb, int wyt) {// 进行编码int codeP1 = 0;int codeP2 = 0;// 编码p1codeP1 = codePoint(p1, wxl, wxr, wyb, wyt);codeP2 = codePoint(p2, wxl, wxr, wyb, wyt);if ((codeP1 | codeP2) == 0) {		// 简取之MidBhline2(p1.x, p1.y, p2.x, p2.y);}else if ((codeP1 & codeP2) != 0) {	// 简弃之return;}else { // 部分课件// 寻找p1的最远可见点if (codeP1 != 0) { // p1不可见VERTEX p11, p22, pmid;p11.x = p1.x;p11.y = p1.y;p22.x = p2.x;p22.y = p2.y;pmid.x = (p11.x + p22.x) / 2;pmid.y = (p11.y + p22.y) / 2;while (abs(p11.x - pmid.x) > 1 || abs(p11.y - pmid.y) > 1) {int cmid = codePoint(pmid, wxl, wxr, wyb, wyt);if (cmid == 0) {// 中点在窗口内部p22 = pmid;}else {			// 中点在窗口外部p11 = pmid;}pmid.x = (p11.x + p22.x) / 2;pmid.y = (p11.y + p22.y) / 2;}p1 = pmid;}// 寻找p2的最远可见点if (codeP2 != 0) { // p2不可见VERTEX p11, p22, pmid;p11.x = p1.x;p11.y = p1.y;p22.x = p2.x;p22.y = p2.y;pmid.x = (p11.x + p22.x) / 2;pmid.y = (p11.y + p22.y) / 2;while (abs(p22.x - pmid.x) > 1 || abs(p22.y - pmid.y) > 1) {int cmid = codePoint(pmid, wxl, wxr, wyb, wyt);if (cmid == 0) {// 中点在窗口内部p11 = pmid;}else {			// 中点在窗口外部p22 = pmid;}pmid.x = (p11.x + p22.x) / 2;pmid.y = (p11.y + p22.y) / 2;}p2 = pmid;}// 从p1 - p2划线MidBhline2(p1.x, p1.y, p2.x, p2.y);}
}

四、效果展示

4.1 裁剪效果

裁剪效果如下：

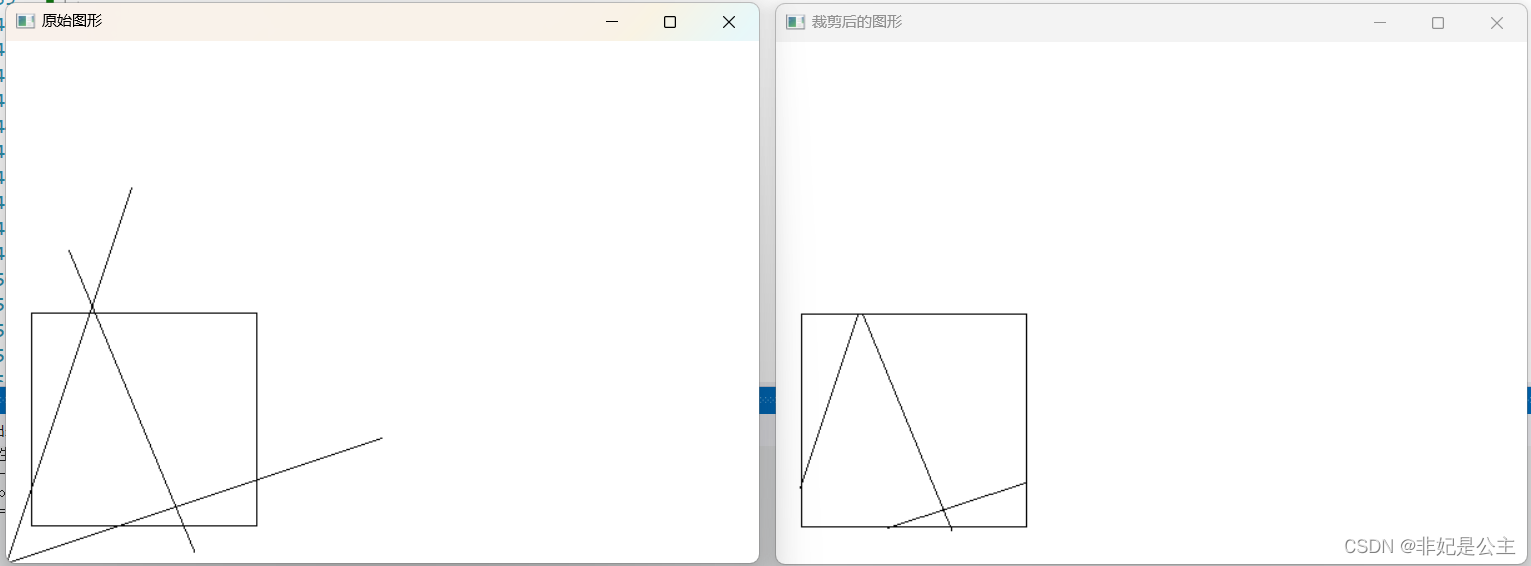
4.2 测试代码

测试代码如下：

void testCropLine() {Bhline(20, 30, 200, 30);Bhline(200, 30, 200, 200);Bhline(200, 200, 20, 200);Bhline(20, 200, 20, 30);VERTEX p1;p1.x = 50;p1.y = 250;VERTEX p2;p2.x = 150;p2.y = 10;cohenCropLine(p1, p2, 20, 200, 30, 200);p1.x = 0;p1.y = 0;p2.x = 100;p2.y = 300;cohenCropLine(p1, p2, 20, 200, 30, 200);p1.x = 0;p1.y = 0;p2.x = 300;p2.y = 100;cohenCropLine(p1, p2, 20, 200, 30, 200);
}// 显示图形
void Display(void) {glClear(GL_COLOR_BUFFER_BIT);		//用当前背景色填充窗口glColor3f(0.0f, 0.0f, 0.0f);// 此处需增加调用基本图形生成函数Bhline(0, 0, 100, 300);Bhline(0, 0, 300, 100);Bhline(20, 30, 200, 30);Bhline(200, 30, 200, 200);Bhline(200, 200, 20, 200);Bhline(20, 200, 20, 30);VERTEX p1;p1.x = 50;p1.y = 250;VERTEX p2;p2.x = 150;p2.y = 10;MidBhline2(p1.x, p1.y, p2.x, p2.y);glFlush();
}// 第2个窗口中的图形绘制
void Displayw(void)
{glClear(GL_COLOR_BUFFER_BIT);glColor3f(0.0f, 0.0f, 0.0f);// 此处进行裁剪testCropLine();glFlush();
}

主函数等其它框架部分与前面(点裁剪)相同，可通过开头链接进行跳转查看，在此不再冗余贴代码片。

五、梁友栋-Barsky算法

这里对另一种线段的裁剪方法进行补充，但不详细展开介绍。

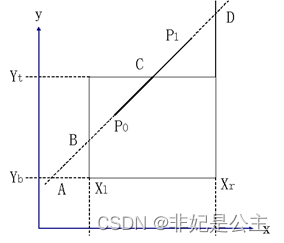
还有一种线段的裁剪方法为梁友栋-Barsky算法，它的基本思想是:

设要裁剪的线段是P0P1。 P0P1和窗口边界交于A,B,C,D四点。从A,B和P0三点中找出最靠近P1的点(P0)。从C,D和P1中找出最靠近P0的点(C)(C)(C)。那么P0C就是P0P1线段上的可见部分。

the end……

有效边表法的多边形扫描转换算法到这里就要结束啦~~到此既是缘分，欢迎您的点赞、评论、收藏！关注我，不迷路，我们下期再见！！

😘😘😘 我是Cherries，一位计算机科班在校大学生，写博客用来记录自己平时的所思所想！
💞💞💞 内容繁杂，又才疏学浅，难免存在错误，欢迎各位大佬的批评指正！
👋👋👋 我们相互交流，共同进步！

注：本文由非妃是公主发布于https://blog.csdn.net/myf_666，转载请务必标明原文链接：https://blog.csdn.net/myf_666/article/details/128508894