【蓝桥杯】2013年第四届省赛-JavaB组-真题+题解
本文已收录至蓝桥杯
部分不会×的借鉴他人答案,暴力解法请勿介意,如果你有更优雅的解法感谢提供
| 题目序号 | 题目标题 | 题目类型 | 考点 | 分值 |
|---|---|---|---|---|
| 题目1 | 世纪末的星期 √ | 结果填空 | 日期API的使用 | 3 |
| 题目2 | 马虎的算式 √ | 结果填空 | 枚举 | 5-6-5 |
| 题目3 | 振兴中华 × | 结果填空 | 递归 | 6-8-8 |
| 题目4 | 黄金连分数 × | 结果填空 | 大数类的使用 | 13-13-12 |
| 题目5 | 有理数类 √ | 代码填空 | 构造器的理解 | 5-5-6 |
| 题目6 | 三部排序 √ | 代码填空 | 排序 | 10-8-11 |
| 题目7 | 错误票据 √ | 编程大题 | 简单数组应用 | 4-5-4 |
| 题目8 | 幸运数 √ | 编程大题 | 数组元素的挪动 | 10-10-12 |
| 题目9 | 带分数 × | 编程大题 | 全排列+check | 17-15-15 |
| 题目10 | 连号区间数 × | 编程大题 | 区间问题 | 27-27-24 |
一. 世纪末的星期
(1) 题目描述

(2) 题解
示例代码整体思路:计算1999年到1999+n*100之间的天数(也可以for循环 1999~9999),然后天数取余7,加上星期5判断是星期几
public class Main {public static void main(String[] args) {// 1.控制年份增长int j = 1;int year;while (true) {// 2.增加周期year = 1999 + j * 100;int day = 0;// 3.判断是否闰年for (int i = 2000; i <= year; i++) {if (i % 4 == 0 && i % 100 != 0 || i % 400 == 0) {day += 366;} else {day += 365;}}// 4. 判断是否为星期日 5+...if ((5 + day) % 7 == 0) {break;}// 5. 下一轮回j++;}// 6. 也就是结果System.out.println(year);}
}
二.马虎的算式
(1) 题目描述

(2) 题解
示例代码整体思路:只会跟着题目要求的等式,嵌套for满足abcde五个参数,在若干个有效的排列组合中找到符合条件的结果。
import java.util.Scanner;public class Main {public static void main(String args[]) {// 1. 记录个数int count = 0;// 2. 凑出等式的5个参数for (int a = 1; a < 10; a++) {for (int b = 1; b < 10; b++) {for (int c = 1; c < 10; c++) {for (int d = 1; d < 10; d++) {for (int e = 1; e < 10; e++) {// 3. 按要求满足5个参数各不相同if (a == b || a == c || a == d || a == e || b == c || b == d || b == e || c == d || c == e | d == e) {continue;}// 4. 判断等式是否成立if ((10 * a + b) * (100 * c + 10 * d + e) == (100 * a + 10 * d + b) * (10 * c + e)) {count++;}}}}}}// 打印结果System.out.println(count);}
}
三. 振兴中华
(1) 题目描述

(2) 题解
示例代码整体思路:题目意思是:从左上角到右下角走方格,路线恰好是从我做起振兴中华的可能种数。
这种走二维方格的,给人第一感觉就是DFS,试错然后回溯。但用在这里,未免小题大做了。如果使用DFS,需要先构造矩阵,然后DFS,然后路线判断。还是有些许的麻烦的。
观察这个矩阵,可以发现一个特点:除边界和第一个字外,其余的字,都是恰好可以接在它的左边或者上面后面的。那么也就是说,可以从上到下开始逐项的累加。其实也就是动态规划。
不难发现,如果使用f(i,j)表示走到第i行,第j列已有的种数,那么状态转移方程是:f(i,j)=f(i + 1, j) + f(i, j + 1)。
如果使用递归的方式来实现这个dp,那么终止条件就是i==3,有f(3,j)=1,或者j==4,有f(i,4)=1
public class Main {public static void main(String[] args) {// 起点int ans = f(0, 0);System.out.println(ans);}private static int f(int i, int j) {// 边界if (i == 3 || j == 4) return 1;return f(i + 1, j) + f(i, j + 1);//将两种走法的路线数相加}
}
四. 黄金连分数
(1) 题目描述

(2) 题解
示例代码整体思路:由于精度限制,需要使用大数记录数值。按照定义可以将其不断分为1/1+x的形式。
import java.math.BigDecimal;
import java.math.RoundingMode;public class Main {public static void main(String[] args) {BigDecimal bd = new BigDecimal(1);for (int i = 0; i < 1000; i++) {bd = bd.add(BigDecimal.ONE);// 数值,位数,四舍五入bd = BigDecimal.ONE.divide(bd, 100, RoundingMode.HALF_DOWN);}System.out.println(bd);}
}
五. 有理数类

// 使用该类的示例:
// Rational a = new Rational(1,3);
// Rational b = new Rational(1,6);
// Rational c = a.add(b);
// System.out.println(a + "+" + b + "=" + c);
//
//
// 请分析代码逻辑,并推测划线处的代码,通过网页提交
// 注意:仅把缺少的代码作为答案,千万不要填写多余的代码、符号或说明文字!!
待补全源代码:
class Rational
{private long ra;private long rb;private long gcd(long a, long b){if(b==0) return a;return gcd(b,a%b);}public Rational(long a, long b){ra = a;rb = b; long k = gcd(ra,rb);if(k>1){ //需要约分ra /= k; rb /= k;}}// 加法public Rational add(Rational x){return ________________________________________; //填空位置}// 乘法public Rational mul(Rational x){return new Rational(ra*x.ra, rb*x.rb);}public String toString(){if(rb==1) return "" + ra;return ra + "/" + rb;}
}
(2) 题解
示例代码整体思路:其实看懂了题目,然后理解了构造方法处代码就会发现其实很简单。
ra:表示分子,rb:表示分母。而构造方法里的gcd递归以及if(k>1)判断则是在确保构造出的分数是最简的形式。由此,我们知道两个分数相加只需要通分成分母相同,再让分子相加即可,这样一样答案就呼之欲出了。最后我们再通过new构造一个分数返回即可。
// return划线处代码
new Rational(ra * x.rb + rb * x.ra, rb * x.rb)
六.三部排序
(1) 题目描述

题目所给源代码:
import java.util.*;
public class Main
{static void sort(int[] x){int p = 0;int left = 0;int right = x.length-1;while(p<=right){if(x[p]<0){int t = x[left];x[left] = x[p];x[p] = t;left++;p++;}else if(x[p]>0){int t = x[right];x[right] = x[p];x[p] = t;right--;//p++; }else{______________;}}show(x);}static void show(int[] x){for(int i=0; iSystem.out.print(x[i] + ",");}System.out.println();}public static void main(String[] args){//int[] x = {25,18,-2,0,16,-5,33,21,0,19,-16,25,-3,0};sort(new int[]{-1,0,1,-2,0,2,-3,0,0,3,-4,-5,4,-6,0,5,6});sort(new int[]{-1,0,-1,-2,0,-2,-3,0,0,-3,-4,-5,-4,-6,0,-5,-6});sort(new int[]{1,0,1,2,0,2,3,0,0,3,4,5,4,6,0,5,6});}
}
(2) 题解
示例代码整体思路:根据题目给的一组测试数据,然后按照已有的逻辑手动模拟一下,猜一下就能发现p++即为解答。
要求:分好组后,负数都靠左端,正数都靠右端,0 在中部。
p <= right:满足条件说明还没遍历到每个数,自然还没排序好,需要继续操作。
x[p] < 0:这里刚开始跟着模拟其实有点小蒙,发现p和left都指向同一个,但是后面遇到0时,发现他们必须要动一个了。动哪个好呢?我们发现if语句里都是x[p]为索引,我们姑且让p++。继续跟着模拟,我们可以发现,left始终标识着最左边一个零,也算是分界点。当我们的p碰到负数时就会与left进行交换,这时负数按照题目所要求被分到了0左边。而left也在指向着下一个非负数。多模拟几轮我们不难发现填入p++即可满足整体要求逻辑。
x[p] > 0时:将p位置数与right位置数进行交换,刚好把正数换到右边了,然后right左移动。为什么p不移动呢?因为right换过去的同样可能为正数,所以需要进行重复判断,最后这个位置只可能是0或负数。
// 划线处else{}内代码
p++
七.错误票据
(1) 题目描述
(2) 题解
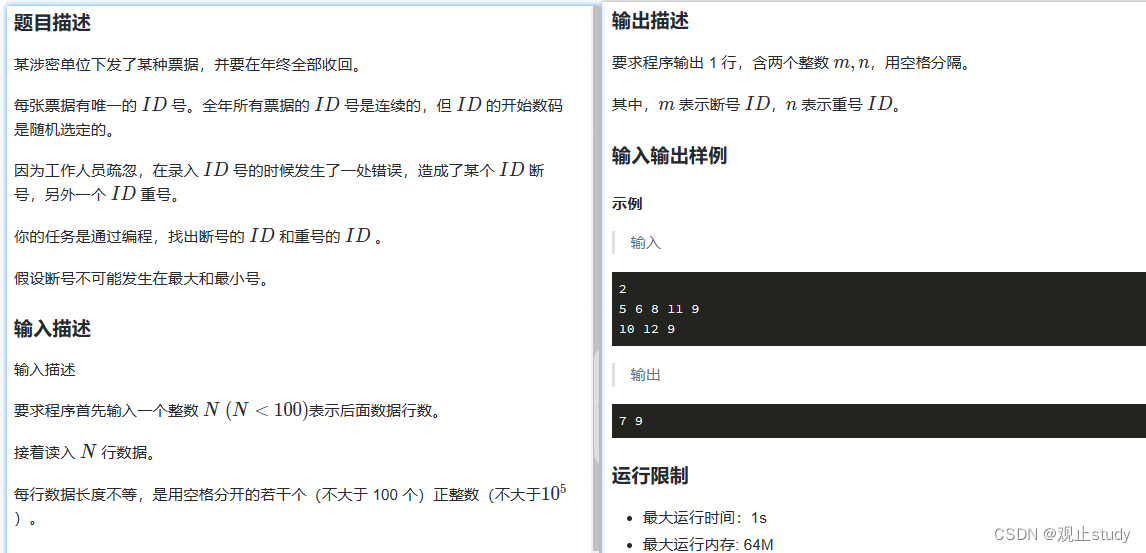
示例代码整体思路:本题是要求找重号和断号。
重号 -> 可以通过哈希表判断数值有没有重复出现。
断号 -> 由于整体是连续的,那么我们从最小值开始遍历,再通过先前记录的哈希表比对肯定能找到中间的断号。
先读取输入的数值,根据split分割为数组,再转为整数,判断如果存在于哈希表则表明找到重号了,如果不存在则存入,同时比较记录最小值。从最小值开始while循环遍历。一一判断是否存在于哈希表,如果不存在说明他就是我们要找的断号。
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);// 1.行数int col = scan.nextInt();// 2.读取消除残余回车符scan.nextLine();// 3.存入行值String[] row = new String[col];for (int i = 0; i < col; i++) {row[i] = scan.nextLine();}// 4.存储2个结果int[] res = new int[2];// 5.记录切割的数值,用于查重和比对断号HashSet hashSet = new HashSet<>();// 6.记录最小值,用于和哈希表比对断号int min = Integer.MAX_VALUE;// 7.切割读取数值for (String s : row) {String[] array = s.split(" ");for (String a : array) {int temp = Integer.parseInt(a);// 8.记录最小值if (min > temp) {min = temp;}// 9.判断是否是重号if (hashSet.contains(temp)) {res[1] = temp;} else {hashSet.add(temp);}}}// 10.比较查找断号,从最小值遍历开始肯定能找到while (true) {if (hashSet.contains(min)) {min++;} else {res[0] = min;break;}}// 11.按照题目要求打印结果格式System.out.println(res[0] + " " + res[1]);}
}
八. 幸运数
(1) 题目描述

(2) 题解
示例代码整体思路:按照规律使用双容器交替排除,找到小于最大值的所有幸运数,然后从中统计要求范围内的个数。
import java.util.Scanner;
import java.util.ArrayList;public class Main {public static void main(String[] args) {// 1. 输入Scanner scan = new Scanner(System.in);int m = scan.nextInt();int n = scan.nextInt();// 2. 存储小于n的所有幸运数ArrayList luckyList = new ArrayList<>(n);// 3. 在初始容器中填入与索引相同的数值ArrayList contain = new ArrayList<>(n);for (int i = 0; i < n; i++) {contain.add(i);}// 4. 因为0号为卡位索引,因此题目开始排除的2在容器中索引为2int j = 2;// 5.由于在不断排除缩小容器,所以当集合内全为幸运数即结束// 后期j即指代幸运数位置,首次特殊处理。while (contain.size() > j) {// 6. 用于交替收集排除后的新数列ArrayList temp = new ArrayList<>(n / contain.get(1));// 为保持数字==索引,同样0卡位temp.add(0);// 7. 按题目所述,留下索引不能被幸运数整除的数for (int i = 1; i < contain.size(); i++) {if (i % contain.get(j) != 0) {temp.add(contain.get(i));}}// 8. 首次特殊处理,2不是幸运数if (luckyList.size() == 0) {luckyList.add(1);} else {// 9. 把每个幸运数加到幸运数容器,并后移到下一个幸运数luckyList.add(contain.get(j++));}// 9. 使用按幸运数剔除后的新数组contain = temp;}// 10. 统计范围内的幸运数个数int count = 0;for (Integer i : luckyList) {if (i > m && i < n) {count++;}}System.out.println(count);}}
九. 带分数
(1) 题目描述
(2) 题解
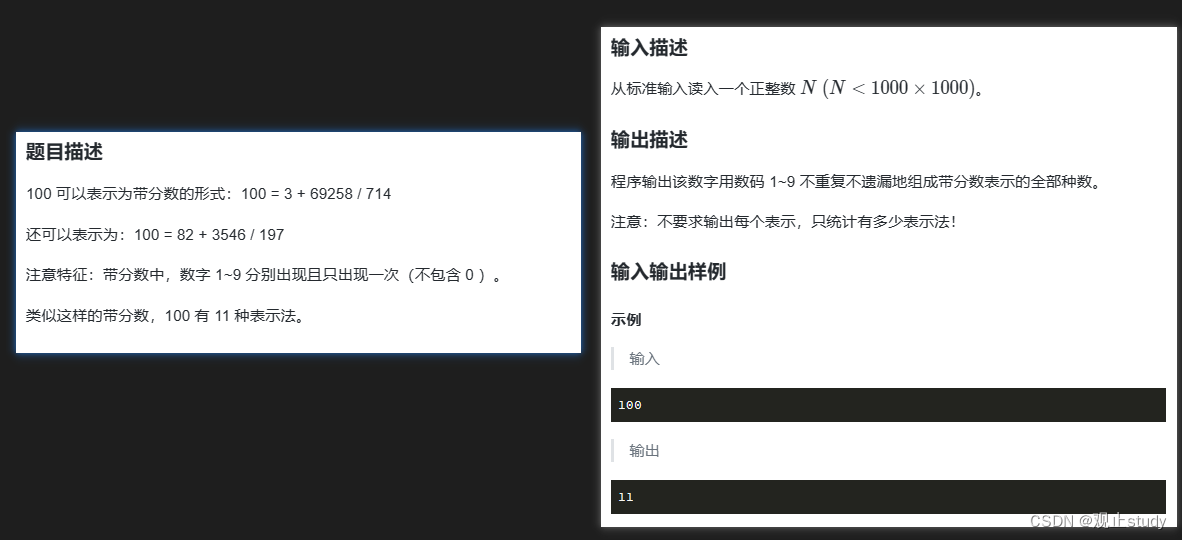
示例代码整体思路:首先题目所说的1-9个数字,不重复,即隐含着实现1-9数字的全排列。全排列实现之后进行加号和除号的位置放置的选择,1-9九个数要实现A+B/C的形式,加号放置此时只能有7种(因为1-9只有8个空格,其中/号占据一个空格,所以+号进行插空只有7种),又+号和/号满足如下关系:
当+号放置在第一个空格时,/号只有7种选择
当+号放置在第二个空格时,/号只有6种选择
当+号放置在第三个空格时,/号只有5种选择
依次类推可以总结如下:
如果+号的选择为:for(int i=1;i<=7;i++)
则/号的选择为:for(int j=i+1;j<=8;j++)
之后进行A+B/C这种形式中A,B,C三个数创建,见下面代码中的cal函数
但在编程时需要注意一点,+号前面的数的值不能大于我们输入的数。
import java.util.Scanner;public class Main {static int N;static int result;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);N = scanner.nextInt();int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};fun(arr, 0);System.out.println(result);}// 1.求1~9的全排列public static void fun(int[] arr, int k) {if (k == 9) {check(arr);} else {for (int i = k; i < 9; i++) {//交换位置,可以封装为方法int t = arr[i];arr[i] = arr[k];arr[k] = t;//下一位fun(arr, k + 1);//回溯t = arr[i];arr[i] = arr[k];arr[k] = t;}}}// 检查带分数公式是否成立public static void check(int[] arr) {//控制a的最小位数和最大位数for (int i = 1; i <= 7; i++) {int a = toInt(arr, 0, i);// 若 a大于N则表明不符合要求if (a >= N) {continue;}// 控制b和c的位数,统计符合条件个数for (int j = 1; j <= 8 - i; j++) {int b = toInt(arr, i, j);int c = toInt(arr, i + j, 9 - i - j);if (b % c == 0 && a + b / c == N) {result++;}}}}// 将全排列数组从下标start到end的数字转为一个整数,并返回public static int toInt(int[] arr, int position, int length) {int t = 1;int answer = 0;for (int i = position + length - 1; i >= position; i--) {answer += arr[i] * t;t *= 10;}return answer;}}
十. 连号区间数
(1) 题目描述
(2) 题解
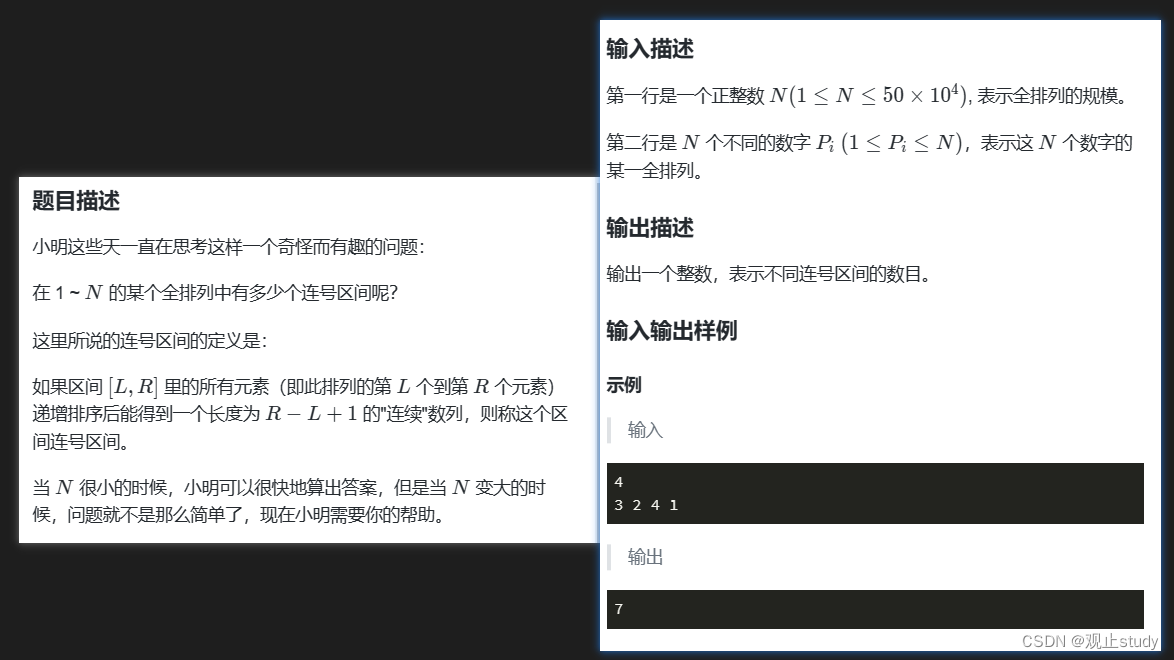
示例代码整体思路:由于其为一串连续数字的全排列。说明其不重复不间断。而要求找的连号区间也是一段排序后连续的数字(包括单个值),可以推断出,若为[L,R]的连续数列,则LR相差位数=最大值-最小值 。就好比1~10。只要他们是连续的,其10和1相差位数必为9。
import java.util.Scanner;public class Main {public static void main(String[] args) {// 1. 初始数值输入Scanner sc = new Scanner(System.in);int N = sc.nextInt();int[] pi = new int[N];for (int i = 0; i < N; i++) {pi[i] = sc.nextInt();}// 2. 统计个数int ans = 0;// 3. 双重for确保遍历到每个长度区间组合for (int i = 0; i < N; i++) {// 4. 先假定起始点为最大值和最小值int max = pi[i], min = pi[i];// 5. 遍历区间for (int j = i; j < N; j++) {// 6. 记录区间内最大值和最小值max = Math.max(max, pi[j]);min = Math.min(min, pi[j]);// 7.若为[L,R]的连续数列,则LR相差位数=最大值-最小值// 比如 2->1,4->2。2 - 1 != 4 - 2 说明其不连续if (j - i == max - min)ans++;}}System.out.println(ans);}
}
