实验01:吃鸡蛋问题
1.实验目的:
通过实验理解算法的概念、算法的表示、算法的时间复杂度和空间复杂度分析;初步学会递归算法和非递归算法的转换。
2.实验内容:
为庆祝三八女生节,学校发给女老师老王发放了n\ge2 个鸡蛋 。老王计划每天吃 2 至 n 个,连续若干天吃完,问老王有多少种吃法。
说明:本题只是数学题,不考虑实际生活中老师的食量 😄。
例: 如果有3个鸡蛋,只有1种正确吃法,因为
$$
\begin{array}{|c|} \hline 吃法 & 第1天 & 第2天 & 第3天 & 正确与否 \\ \hline 1 & 3个 & / & / & 正确\\ 2 & 2个 & 1个 & / & 错误\\ 3 & 1个 & 2个 &/ & 错误\\ 4 & 1个 & 1个 & 1个 & 错误\\ \hline \end{array}
$$程序输入输出示例:
输入(鸡蛋个数):3
输出(正确吃法数):1
3.实验要求:
编制程序并对其时间复杂度和空间复杂度进行分析,实现递归版本和非递归版本。
\square 基础性实验 \square 综合性实验 \boxtimes 设计性实验
实验报告正文
一、问题分析(模型、算法设计和正确性证明等)
设老王吃完n个鸡蛋的方法有f(n)种,则有递归式:
情况1:n=1
不符合题意所以无合法吃法。
情况2:n=2
老王每天至少吃2个鸡蛋所以只有一种吃法。
情况3:n>2
老王吃完鸡蛋的情形可分为以下两种:
-
最后一天吃了2个鸡蛋
-
最后一天吃了3个及以上鸡蛋
对于情形1,只考虑剩下n-2个鸡蛋的吃法即可,即f(n-2)。
对于情形2,因为最后一天吃的鸡蛋数\geq 3个,所以减少1个也是合法的吃法,所以该情形的吃法有f(n-1)种。
二、算法设计复杂度分析(伪代码,不要粘贴源码)
-
递归算法

下求解递归算法的时间复杂度,设规模为n问题所需的计算时间为T(n),则有:
$$$$
通过微分方程法求得方程的解:
$$$$
下讨论递归算法的空间复杂度,每次返回函数本身都会开辟新的栈空间,故递归树的高度即为该算法所用空间。递归出口为1和2,递归树高度为n-1,所以空间复杂度为\theta (n)。
-
非递归算法
-

下讨论非递归算法的时间复杂度,设规模为n的问题所需的计算时间为T(n),则有:
$$
$$下讨论非递归算的空间复杂度,该算法仅使用两个整型变量(伪代码中a,b)辅助运算,故空间复杂度为\theta(1)。
三、实验结果记录和分析(测试向量的测试时间运行结果)
-
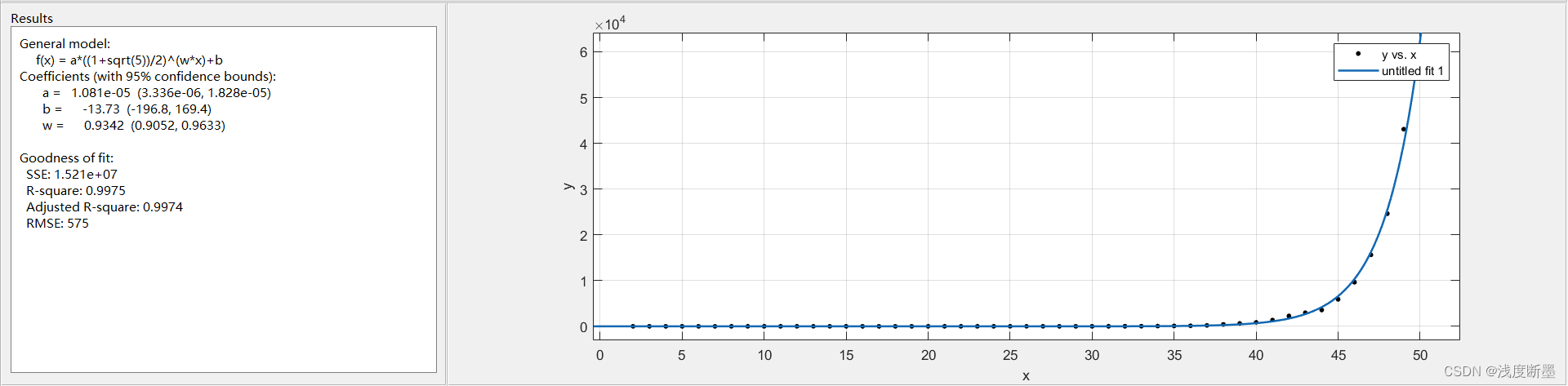
递归算法
鸡蛋数(个) 结果(种) 运行时间(ms) 2 1 0.0003 7 8 0.0003 12 89 0.0015 17 987 0.0149 22 10946 0.1275 27 121393 0.8093 32 1346269 8.9908 37 14930352 14.5162 42 165580141 1106.4063
-
非递归算法
鸡蛋数(个) 结果(种) 运行时间(ms) 2 1 0.0002 7 8 0.0001 12 89 0.0001 17 987 0.0001 22 10946 0.0002 27 121393 0.0001 32 1346269 0.0001 37 14930352 0.0002 42 165580141 0.0002 101 218922995834555200000 0.0004 1001 2.686381002448534e208 0.0028 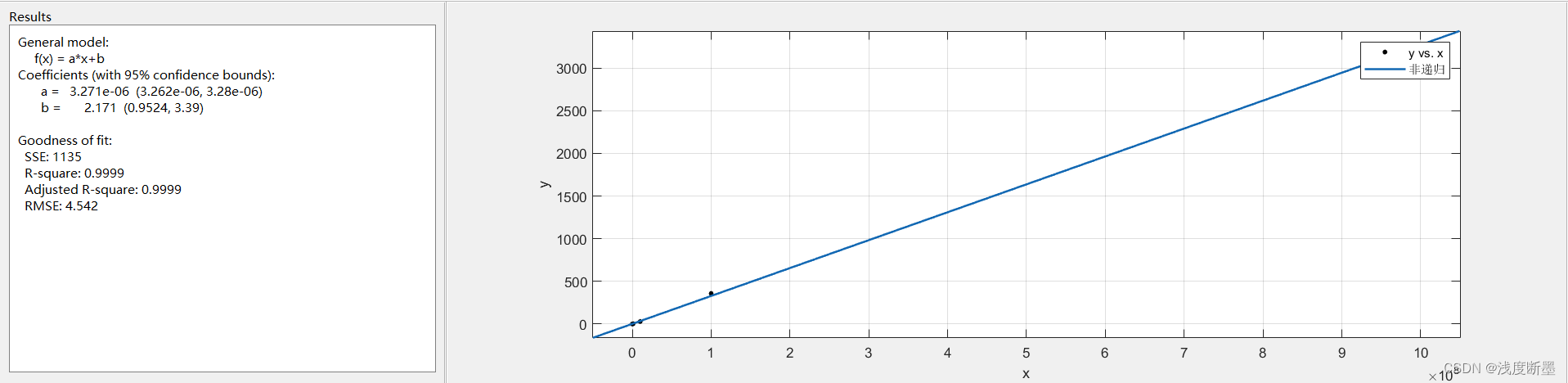
四、总结(可描述出现的问题和解决方法、经验和反思等)
此问题应与整数划分区别开,整数划分(最小数不少于2)只计算划分数即可,本问题还需计算每个划分种不同排列,例如n=7时,\{2,2,3\}是一种合法的整数划分,而\{2,2,3\},\{2,3,2\},\{3,2,2\}都是合法的吃鸡蛋方式,记3种,故两者并不相同。
递归算法的思路更加接近我们思考一个问题的方式,结构清晰,可读性强。可用数学归纳等方法证明其正确性,设计算法及调试很方便。但是效率很低,时间空间复杂度都高于非递归算法。
本次实验中可将递归算法写作以下非递归算法:
memo = dict({1:0,2:1});
def f(n):if n in memo:return memo[n]else:memo[n] = f(n-1) + f(n-2);return memo[n]时间复杂度为O(n^2),空间复杂度为O(n),但是本实验中采用进一步优化的迭代算法改善算法效率。
